à‰tude des différentes lois de commande pour un robot manipulateur à 6DDL comportant une liaison prismatique

I.6. Espace de travail

I.6.1. Définition

L'espace de travail est l'ensemble des positions et /ou orientations accessible par l'organe terminal du robot.

Le volume ou l'espace de travail d'un robot dépend généralement de trois facteurs :

- De la géométrie du robot,

- De la longueur des segments,

- Du débattement des articulations (limité par des butées)

Soit une configuration articulaire donnée et soit X l'élément de l'espace opérationnel correspondant, tel que :

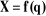
On note Q l'ensemble des configurations accessibles compte tenu des butées articulaires, Par conséquent, Q sera appelé domaine articulaire.

L'image de Q par le modèle géométrique direct f définit l'espace de travail W du robot:

(I-21)

Dans le cas général,  Les orientations de l'organe terminal n'apparaissent pas dans la définition de ce volume de travail car ce n'est pas facile de les représentées.

W est donc la projection dans l'espace des positions [FIS 04].

Comme on l'a définie précédemment, la position de l'organe terminal dans le repère atelier est donnée par le vecteur position P dans la matrice de transformation ^FT_E.

On a développé un programme qui a comme paramètres d'entrée les limites articulaires de chaque articulation et comme sortie toutes les configurations possibles (les positions) de l'organe terminal, l'algorithme associé à ce programme est : [BEN 06]

Début

Entrer (q_min et q_max) pour chaque articulation ;

i =1

Pour q₁ allant de q_min à q_max faire

Pour q₂ allant de q_min à q_max faire

......

.......

Pour q_n allant de q_min à q_max faire

px(i)=f(q)

py(i)=f(q)

pz(i)=f(q)

i=i+1

fin pour

......

fin pour

fin pour

Sortie (Px,Py,Pz)

fin du programme

I.6.2. Application numérique

Si on admet que chaque liaison rotoïde permet une rotation d'un tour complet (2) et que l'origine O_E du repère outil est le point de référence, dans l'absence des butées articulaires et sans tenir compte les positions singulières, l'espace de travail dans ce cas est une sphère creuse du centre O₂ l'origine du repère R₂ et de rayons intérieur et extérieur L-L6 et L+r3 (où L=RL4+L2), Figure (I.8).

La figure (I.9), montre la représentation de cette espace dans le cas où :

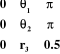
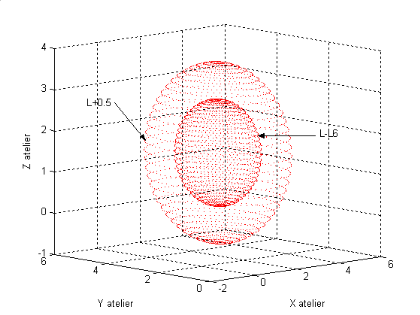
Figure I.8. L'espace de travail du robot lorsque : 0<_i<2ð, 0<r3<0.5

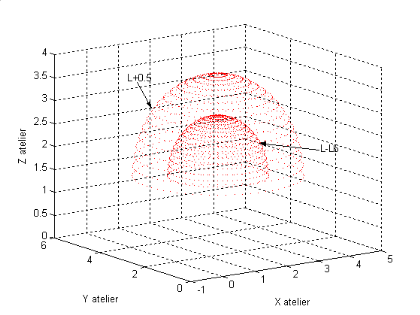
Figure I.9.  L'espace de travail du robot lorsque : 0<1,2<ð, 0<4,5 <2ð, 0<r3<0.5