I.5.
Le MGD du robot
I.5.1 La chaîne
cinématique du robot
Le robot manipulateur utilisé dans ce travail est de
type série à 6 degrés de liberté, constitué
par 6 corps mobiles supposés parfaitement rigides .le porteur est de
type RRP et le poignet comporte trois rotations d'axes concourants, ce robot a
une position connue par rapport à un repère atelier et le dernier
repère choisi pour le calcul du MGD est celui de l'outil .voir
figure (I.3)
Figure I.3. La chaîne
cinématique du robot
RRPRRR
r1
L6
Z2
X4 X5
X6
Z1 X2
X3
X1
Z5
Z4 Z6
1
2
4
5
6
r3
Z3
RL4
ZE
XE
il
Z0
X0
6TE
0T6
ZF
XF
YF
F T0
L2
Ce robot est caractérisé par les
paramètres suivants :
|
j
|
|
|
d
|
|
r
|
|
1
|
0
|
0
|
d1
|
1
|
r1
|
|
2
|
0
|
/2
|
0
|
2+ /2
|
0
|
|
3
|
1
|
/2
|
0
|
0
|
L2+r3
|
|
4
|
0
|
0
|
0
|
4
|
RL4
|
|
5
|
0
|
-/2
|
0
|
5
|
0
|
|
6
|
0
|
/2
|
0
|
6
|
0
|
Tableau I.1 Paramètres
géométriques relatifs au mécanisme
Le long du projet, on a attribué aux
différentes longueurs du mécanisme, les mêmes valeurs qui
sont :
r1 =1.5 m
L2 = 0.75 m
RL4 = 0.75 m
L6 = 0.20 m
La transformation du repère  au repère  et celle du repère  au repère  sont représentées par les translations et les rotations
suivantes :
 (I-15)
(I-16)
Le vecteur des variables articulaires comporte cinq angles
(rad) et une translation (m), il est exprimé comme suit: (I-17)
Le calcul des matrices de transformation homogène sous
Maple nous a donné :
 
     
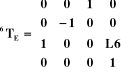
avec : 
(I-18)
Le modèle géométrique direct est
donné selon la relation :
(I-19)
Puisque on a choisi de représenter les rotations par
les angles de RTL, Le vecteur des coordonnées
opérationnelles X simplifié (en fonction de
q), extrait de l'expression de la matrice , est comme suit:
(I-20-a)
(I-20-b)
avec :
 (I-21)
I.5.2. Application
Puisque X est en fonction de
q et des paramètres de , on a joué sur les valeurs de ces variables pour obtenir
différentes configurations de l'effecteur. Les figures (I.4),
(I.5), (I.6) et (I.7) montrent les résultats
et les coordonnées opérationnelles obtenues pour plusieurs
positions et mouvements simples.
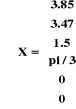
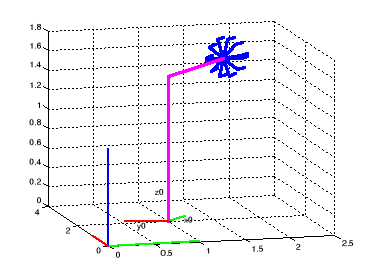
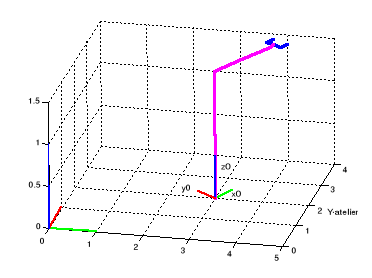
Figure I.4. Le robot à
l'état de repos où d1=3, y1=2, 0=pi/3
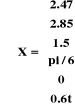
Figure I.5. La position du robot
lorsque : d1=1, y1=2, 0=pi/6, 6=0.6*t, t=0:5
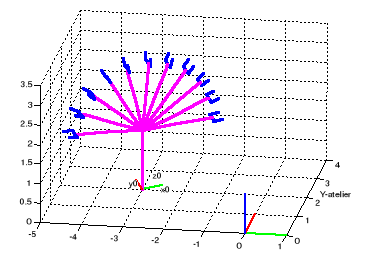
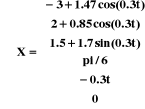
Figure I.6.la
position du robot lorsque : d1= -3, y1=2, 0=pi/6, 2=0.3*t, t=0:5
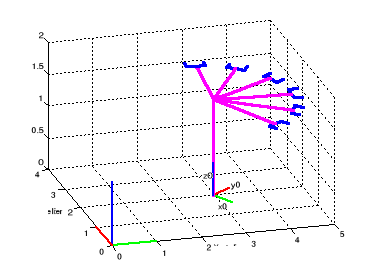
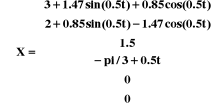
Figure I.7.
La position du robot lorsque : d1=3, y1=2, 0= -pi/3,
1=0.5*t, t=0:5
| 
