IV.3.2.
Formalisme de Lagrange
Les équations de Lagrange permettent d'obtenir
directement les relations entre les efforts moteurs aux articulations et les
mouvements. Par rapport aux équations de Newton, on perd au passage les
informations sur les efforts de réaction aux articulations qui sont
utiles au dimensionnement des parties mécaniques, mais n'interviennent
pas dans un modèle utile à la commande automatique puisque les
corps sont supposés indéformables [CHE 03].
Il s'agit de n équations
différentielles non linéaires du second ordre obtenues à
partir de :
(IV-17)
avec :
L est le Lagrangien du système, c'est
la différence entre  l'énergie cinétique du système, et  l'énergie potentielle du système.
(IV-18)
Pour tous les systèmes mécaniques,
l'énergie cinétique est une forme quadratique des
vitesses :
 (IV-19)
où  est une matrice symétrique définie positive dépendant des masses
et des inerties de chaque corps du mécanisme, et de la configuration
q . En effet :
(IV-20)
et on a vu que les vitesses de translation et de rotation de
chaque corps sont des fonctions linéaires des vitesses articulaires.
D'autre part, l'énergie potentielle est fonction de la
configuration du mécanisme:
Il en résulte que les équations de Lagrange
peuvent s'écrire :
(IV-21)
où le premier vecteur représente les forces ou
couples d'inertie sur les articulations motorisées, le deuxième
(du second degré par rapport aux vitesses) correspond aux effets
centrifuges et de Coriolis, le troisième traduit les efforts dus
à la pesanteur et aux ressorts. [éEF 05]
Le modèle dynamique lorsqu'on applique la force  peut s'écrit sous la forme :
 (IV-22)
où :
La matrice d'inertie est obtenue directement à partir
de l'expression de l'énergie cinétique  ; L'élément  est égal au coefficient de  dans l'expression de l'énergie cinétique, tandis que
l'élément  est égal au coefficient de .
Le calcul des éléments de C se
fait à partir du symbole de Christophell  selon la relation :
 (IV-23)
Le calcul de Q se fait à partir de
l'énergie potentielle :
(IV-24)
Si on prend en compte l'effet du frottement dans les liaisons
sur le mouvement, on doit ajouter au deuxième membre de l'expression
(IV-24) le vecteur .
L'équation dynamique devient :
 (IV-25)
Si on tient compte des inerties des actionneurs , l'élément  de la matrice d'inertie doit être augmenté de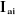
Il est évident que pour trouver les
éléments de M, C et
Q, il faut tout d'abord calculer les énergies
cinétique et potentielle de tous les corps du
robot.
Calcul de l'énergie
cinétique :
L'expression de l'énergie cinétique total d'un
système composé de n corps rigides
est :
(IV-26)
Où  désigne l'énergie cinétique du corps , qui s'exprime par :
(IV-27) Etant donné que :
(IV-28) Et sachant que :
(IV-29) La relation (IV-28)
devient :
 (IV-30) Dans
l'équation (IV-32), tous les éléments doivent être
exprimés dans le même repère. La façon la plus
simple est de les exprimer dans le repère
Ri, l'équation devient donc :
 (IV-31)
Le calcul de  et de  se fait par la relation (III-11).
Calcul de l'énergie
potentielle :
L'énergie potentielle s'écrit :
 (IV-32) En projetant
les vecteurs de cette relation dans , on obtient :
 (IV-33)
Les énergies cinétiques et potentielles
étant linéaires par rapport aux paramètres inertiels, le
modèle dynamique l'est également.
| 
