Chapitre IV
L'étude dynamique du robot
IV.1.
Introduction
Tandis que les équations cinématiques
décrire le mouvement du robot sans considération des forces et
des moments produisant le mouvement, les équations dynamiques
décrivent explicitement le rapport entre les couples (et/ou forces)
appliqués aux actionneurs et le mouvement (positions, vitesses et
accélérations articulaires).
Les principaux problèmes dans la dynamique du robot
sont [FEA 07] :
· La dynamique directe : (donner les
forces et établir les accélérations), elle est
employée principalement pour la simulation.
· La dynamique inverse : (donner les
accélérations, établir les forces), elle a des diverses
utilisations, incluant : commande en ligne des mouvements et des forces de
robot, conception de trajectoire et optimisation, conception du
mécanisme du robot et le calcul des coefficients de l'équation
du mouvement.
· L'identification des paramètres inertiels.
IV.2. Notation
Les principales notations utilisées sont les
suivantes :
 : la masse du corps Ci : la masse du corps Ci
 : accélération de la pesanteur. : accélération de la pesanteur.
 : vecteur d'origine : vecteur d'origine  et d'extrémité et d'extrémité égal à égal à  . .
 : vecteur d'origine : vecteur d'origine  et d'extrémité et d'extrémité égal à égal à  . .
 et et  : vitesse et accélération de rotation du corps
Ci. : vitesse et accélération de rotation du corps
Ci.
 et et  : vitesse et accélération du point : vitesse et accélération du point 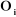
 et et  : vitesse et accélération du centre de
gravité (Gi) du corps
Ci : vitesse et accélération du centre de
gravité (Gi) du corps
Ci
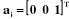
 résultante des forces extérieures sur le corps
Ci. résultante des forces extérieures sur le corps
Ci.
 moment des effort extérieurs exercés sur le corps
Ci autour de
Oi. moment des effort extérieurs exercés sur le corps
Ci autour de
Oi.
 vecteur d'origine Oi et
d'extrémité Gi. vecteur d'origine Oi et
d'extrémité Gi.
 le tenseur du vecteur le tenseur du vecteur  tel que : tel que :
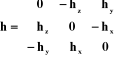
 :désigne le produit vectoriel. :désigne le produit vectoriel.
 tenseur d'inertie du corps Ci par rapport
au repère Ri qui s'exprime
par : tenseur d'inertie du corps Ci par rapport
au repère Ri qui s'exprime
par :
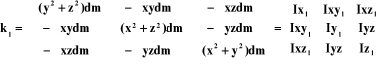
 tenseur d'inertie du corps Ci par rapport
à un repère parallèle à
Ri et d'origine
Gi. tenseur d'inertie du corps Ci par rapport
à un repère parallèle à
Ri et d'origine
Gi.
 et et  résultante et moment du torseur dynamique exercé sur le
corps Ci par son
antécédent et par l'actionneur i. résultante et moment du torseur dynamique exercé sur le
corps Ci par son
antécédent et par l'actionneur i.
 et et  résultante et moment du torseur dynamique exercé par le
corps Ci sur l'environnement. résultante et moment du torseur dynamique exercé par le
corps Ci sur l'environnement.
 , avec , avec  le paramètre de frottement sec de l'articulation
i. le paramètre de frottement sec de l'articulation
i.
 , avec , avec  le paramètre de frottement visqueux de l'articulation
i le paramètre de frottement visqueux de l'articulation
i
IV.3. Le modèle dynamique
inverse (MDI)
Le modèle dynamique inverse (ou le modèle
dynamique tout court) d'un robot permet de déterminer les
équations du mouvement, c'est-à-dire : la relation entre les
couples appliqués aux actionneurs et les positions, vitesses et
accélérations articulaires [FEA 07].
Il est exprimé sous la forme :
 (IV-1)
(IV-1)
Dans cette équation  sont, respectivement, les vecteurs de position, vitesse,
accélération et force, dans l'espace articulaire. Chacun est
un vecteur de dimension n. Les variables de force sont
définies tels que sont, respectivement, les vecteurs de position, vitesse,
accélération et force, dans l'espace articulaire. Chacun est
un vecteur de dimension n. Les variables de force sont
définies tels que  est la puissance fournie par est la puissance fournie par  au système. Ainsi, au système. Ainsi,  et et  qualifiés comme ensemble de variables
généralisées de vitesse et de force pour le
système. qualifiés comme ensemble de variables
généralisées de vitesse et de force pour le
système.
 est un vecteur (6) ; dénote la force externe agissant sur le
robot, dû au contact avec l'environnement ,ainsi le robot exerce une
force de est un vecteur (6) ; dénote la force externe agissant sur le
robot, dû au contact avec l'environnement ,ainsi le robot exerce une
force de  sur l'environnement. sur l'environnement.
Les deux principaux formalismes utilisés pour obtenir
les équations différentielles qui décrivent le
comportement d'un mécanisme à plusieurs corps articulés
sont le formalisme de Newton (théorèmes généraux de
la mécanique classique) et celui de Lagrange. [AIS 06]
IV.3.1.
Formalisme de Newton Euler
Cette méthode est fondée sur une double
récurrence ; la récurrence avant de la base du robot vers
l'effecteur, calcule successivement les vitesses et accélérations
des corps, puis leur torseur dynamique, une récurrence arrière
de l'effecteur vers la base, permet le calcul des couples des actionneurs en
exprimant pour chaque corps le bilan des efforts. [KHA 99]
Les équations de Newton Euler expriment le torseur
dynamique en  des efforts extérieurs sur un corps i par les
équations : [CRA 89] des efforts extérieurs sur un corps i par les
équations : [CRA 89]
 (IV-2)
(IV-2)
Cette méthode permet d'obtenir un MDI non
linéaire par rapport aux paramètres inertiels, pour qu'il soit
linéaire, le MDI doit être calculé en exprimant le torseur
dynamique des efforts extérieurs en plutôt que plutôt que . .
Les équations de Newton Euler ainsi modifiées
s'écrivent :
 (IV-3)
(IV-3)
· Récurrence avant : elle
permet de calculer  et et  à partir de la relation (IV-3). Pour ce faire, il faut
calculer à partir de la relation (IV-3). Pour ce faire, il faut
calculer . .
Les formules de composition des vitesses donnent :
 (IV-4)
(IV-4)
La dérivée de l'équation (IV-4) par
rapport au temps s'écrit :
 (IV-5) (IV-5)
Ce qui donne :
 (IV-6) (IV-6)
On peut finalement calculer et et , on initialise cette récurrence par , on initialise cette récurrence par et et . .
· Récurrence arrière :
Les équations composant la récurrence arrière
sont obtenues à partir du bilant des efforts sur chaque corps,
écrit à l'origine , on obtient (FigureIV.1) , on obtient (FigureIV.1)
i-1
i+1
Oi+1
Oi
Gi
Li+1
Si
i
-fi+1
fi - fei
 (IV-7)
(IV-7)
Figure IV.1.
Bilan des efforts au centre de gravité
On peut faire intervenir l'effet de la gravité
sans avoir à la prendre en compte dans le bilan des efforts, pour
cela on prend:
 (IV-8)
(IV-8)
D'où l'on tire les équations suivantes :
 (IV-9)
(IV-9)
On obtient alors les couples aux actionneurs  en projetant, suivant la nature de l'articulation i,
les vecteurs en projetant, suivant la nature de l'articulation i,
les vecteurs ou ou sur l'axe du mouvement : sur l'axe du mouvement :
 (IV-10)
(IV-10)
Les frottements doivent être pris en compte dans
l'équation dynamique. Le modèle du type frottement sec (ou de
Coulomb) fait l'hypothèse d'un couple constant de frottement en
opposition au mouvement. Au début du mouvement (vitesse nulle), un
couple supérieur au couple de frottement sec doit être
développé pour amorcer le mouvement. De nombreuses études
ont été réalisées afin de mieux analyser les
frottements, menant à l'approximation suivante [VIV 04] :
 (IV-11) (IV-11)
On ajoute à 'équation (IV-10) les termes
correctifs représentant l'effet des frottements et des inerties des
actionneurs, , ce qui nous donne la relation suivante : , ce qui nous donne la relation suivante :
 (IV-12)
(IV-12)
Les inerties des actionneurs sont calculées comme
suit :
 (IV-13)
(IV-13)
 est le moment d'inertie du rotor de l'actionneur i, est le moment d'inertie du rotor de l'actionneur i,
 est le rapport de réduction de l'axe i
égal à est le rapport de réduction de l'axe i
égal à  et et  désigne la vitesse du rotor de l'actionneur i. désigne la vitesse du rotor de l'actionneur i.
On déduit directement de l'équation (IV-9)
que les termes  et et ne dépendent que des paramètres inertiels du corps
i et de ceux des corps situées en aval qui sont
introduit par les termes ne dépendent que des paramètres inertiels du corps
i et de ceux des corps situées en aval qui sont
introduit par les termes  et et  de la récurrence. de la récurrence.
Pour utiliser pratiquement l'algorithme de Newton Euler
exposé ci-dessus, il faut projeter dans un même repère les
vecteurs et tenseurs qui apparaissent dans une même équation. [BOI
88]
Les équations de la récurrence avant peuvent
être présentées par l'algorithme suivant:
· Récurrence avant :
Conditions initiales :
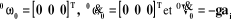
 (IV-14) (IV-14)
 (IV-15)
(IV-15)
Les équations de la récurrence arrière
peuvent être présentées par l'algorithme suivant:
· Récurrence
arrière :
Conditions initiales:
  (IV-16) (IV-16)
Dans cette formulation (Newton Euler), l'effet de la pesanteur
est introduit par une accélération verticale de la base du robot.
Si le robot manipulateur est situé sur un véhicule dont le
mouvement est connu, on peut donc également introduire les fonctions du
temps correspondantes (vitesses et accélérations) dans les
premières récurrences directes qui partent de la base [TEC
07].
| 


