III.2.2. Calcul direct de la
matrice Jacobienne
On peut utiliser une méthode très
répandue pour le calcul cinématique, qui permet d'obtenir la
matrice jacobienne par un calcul direct fondé sur l'influence que
produit chaque articulation d'ordre  de la chaîne sur le repère terminal de la chaîne sur le repère terminal . .
a) articulation prismatique
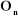
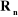
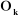
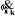
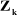
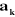
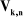
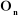
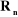
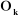
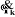
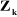
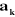
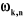
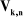
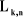
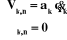
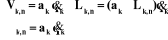
z j
On peut calculer  en considérant séparément les cas d'une
articulation prismatique et d'une articulation rotoïde: en considérant séparément les cas d'une
articulation prismatique et d'une articulation rotoïde:
Figure
III.1. Influence du type de l'articulation sur le repère
terminal
où :
 : désigne le vecteur d'origine et d'extrémité : désigne le vecteur d'origine et d'extrémité
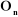
 : est le vecteur unitaire porté par l'axe : est le vecteur unitaire porté par l'axe  de l'articulation de l'articulation  . .
En introduisant le coefficient binaire , les vecteurs , les vecteurs  s'écrivent : s'écrivent :
 (III-5)
(III-5)
Grâce au théorème de la composition des
vitesses, on peut sommer toutes les contributions élémentaires de
chaque articulation afin d'obtenir les vecteurs finaux des vitesses de
translation et de rotation  du repère terminal par l'expression : du repère terminal par l'expression :
 (III-6)
(III-6)
Par identification avec la relation (III-2), la matrice
Jacobienne exprimée dans le repère , notée , notée , s'écrit : , s'écrit :
 (III-7) (III-7)
D'une façon générale,
projetée dans le repère , la matrice jacobienne notée , la matrice jacobienne notée s'écrit : s'écrit :
 (III-8) (III-8)
En remarquant que :
 (III-9)
(III-9)
avec :
 · : matrice d'orientation de dimension · : matrice d'orientation de dimension  du repère du repère  dans le repère dans le repère , ,
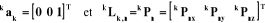
· On calcule alors la  colonne de la matrice Jacobienne, notée colonne de la matrice Jacobienne, notée , projetée dans le repère , projetée dans le repère  par la formule : par la formule :
 (III-10) (III-10)
où :
·
isk,
ink et
iak : sont
respectivement le  vecteurs de la matrice
iAk. vecteurs de la matrice
iAk.
·
kPnx et
kPny : sont
respectivement la  composantes du vecteur composantes du vecteur qui est la quatrième colonne de qui est la quatrième colonne de  calculée précédemment par le modèle
géométrique direct. calculée précédemment par le modèle
géométrique direct.
III.2.3. le calcul du MCD par les équations de
récurrence
Connaissant Jn
les vitesses de translation et de rotation du repère
Rn peuvent être obtenus à partir de la
relation (III-2). De point de vue nombre d'opérations, il est cependant
plus judicieux d'utiliser les équations de récurrence
suivantes :
 (III-11)
(III-11)
On initialise la récurrence avec les vitesses
opérationnelles  et et  de la base du robot. de la base du robot.
La vitesse obtenue dans ce cas est  , pour trouver , pour trouver  on fait la projection de ce vecteur dans le repère
R0 : on fait la projection de ce vecteur dans le repère
R0 :
 (III-12)
(III-12)
Le calcul du MCD, par la matrice jacobienne ou bien par les
équations de récurrence, donne le vecteur  où où  est la dérivée par rapport au temps du vecteur de
position est la dérivée par rapport au temps du vecteur de
position , mais le , mais le  ne représente pas la dérivée de l'orientation, il
faut trouver donc une relation entre les coordonnées
opérationnelles X et le modèle
cinématique. ne représente pas la dérivée de l'orientation, il
faut trouver donc une relation entre les coordonnées
opérationnelles X et le modèle
cinématique.
| 


