à‰tude des différentes lois de commande pour un robot manipulateur à 6DDL comportant une liaison prismatique

III.2.4. la jacobienne analytique 

La matrice jacobienne développée ci-dessus s'appelle parfois la jacobienne géométrique pour la distinguer de la jacobienne analytique, dénoté J_a(q), qui est basée sur une représentation minimale pour l'orientation du repère de l'effecteur .

Soit une représentation de la situation du repère R_n dans R₀, où x_p représente les trois coordonnées opérationnelles de position et x_r représente les coordonnées opérationnelles d'orientation, les vitesses opérationnelles sont donc , on doit trouver la relation entre ces vitesses et les vecteurs vitesses telle que :

(III-13)

Ou sous forme matricielle :

(III-14)

Partant de la relation (III-13), on peut déduire que :

(III-15)

avec :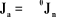

En général, la sous matrice est égale à la matrice unité I₃ car les coordonnées opérationnelles de position sont simplement les coordonnées cartésiennes de la position de l'outil. Par contre, la matrice dépend du choix effectué pour les coordonnées opérationnelles de rotation. Cette matrice est parfois singulière ; par exemple dans le cas des quaternions d'Euler, elle est tout simplement non carrée c.-à-d. non inversible. Les cas pour lesquels la matrice complète n'est pas inversible constituent des singularités mathématiques : ces singularités sont uniquement dues au choix des coordonnées opérationnelles, elles n'ont rien à voir avec le manipulateur lui même. [SPO 04]

Comme il est défini dans le premier chapitre le vecteur d'orientation qu'on a choisi est :

dans ce cas [KHA 99]:

(III-16)

et (III-17)

Singularité lorsque.

III.2.5. Utilisation de la matrice jacobienne 

La matrice jacobienne est l'une des quantités les plus importantes dans l'analyse et la commande du mouvement de robot. Elle survient pratiquement dans chaque aspect de manipulation robotique : dans la planification, dans la détermination des configurations singulières, dans la dérivation des équations dynamiques du mouvement, et dans la transformation des forces et les couples du terminal aux joints de manipulateur [SPO 04]

III.2.5. 1. Calcul des efforts statiques

À partir du modèle cinématique, on peut écrire le modèle différentiel :

(III-18)

Supposons que les variables q_i soient directement les variables associées aux déplacements relatifs des moteurs rotatifs ou linéaires. Chacun de ces derniers exerce une force ou un couple noté, d'où pour l'ensemble des degrés de liberté un vecteur des efforts  . (III-19)

Si l'on note F le vecteur à six composantes de la force et du moment exercés par l'organe terminal sur l'environnement, le principe des travaux virtuels permet d'écrire :

(III-20)

d'où : (III-21)

qui donne la répercussion des efforts moteurs sur l'environnement, en dehors des singularités.

On utilise la matrice jacobienne ou selon que l'effort F est défini dans le repère R_n ou dans R₀ respectivement. [TEC 07]

Dans le cas inverse, où on veut calculer le que doivent fournir les actionneurs pour que l'organe terminal puisse exercer un effort F, on peut déduire à partir de la relation (III-21) que :

(III-22)