II.5.
Application
On a prend comme exemple de trajectoire, la poursuite d'une
tache de soudure d'un objet de forme cylindrique associé à un
repère Robj, ce dernier est
relié au repère atelier par la matrice : :
 (II-28)
(II-28)
La description du trajet de l'outil par rapport à
Robj est donnée par la transformation
homogène : :
 (II-29) (II-29)
la position désirée de l'outil par rapport au
repère atelier est donc :

 (II-30) (II-30)
avec :
pas signifié le pas du temps
choisi : 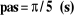
Les résultats de cette simulation sont montrés
par les figures (II.2 et II.3),
ils ont validé le MGI calculé.
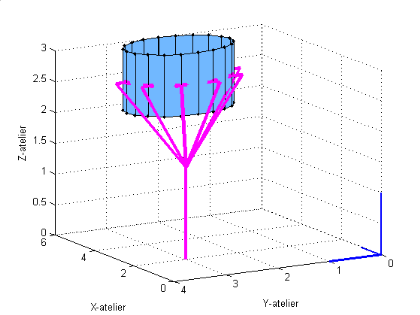
Figure
II.2. Suivi de la trajectoire donnée
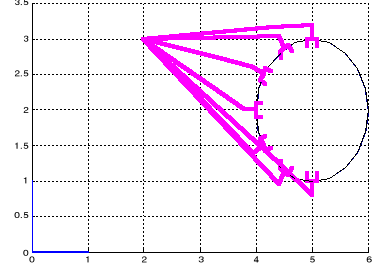
Figure II.3.
Suivi de la trajectoire donnée (vue de dessus)
II.5.
Conclusion
On a exposé dans ce chapitre
la méthode de Paul pour le calcul du MGI, cette méthode
intuitive en ce sens qu'elle laisse à l'utilisateur le choix des
équations à résoudre, elle est applicable à un
grand nombre de chaînes cinématiques possédant surtout des
paramètres géométriques particuliers : distance
nulles ou angles dont les sinus et cosinus sont égaux à 0, 1, -1,
en plus, cette méthode analytique donne toutes les solutions possibles
du modèle géométrique inverse.
Nous avons également résolu le
modèle géométrique inverse du robot proposé
grâce à cette méthode.
Après cette modélisation
géométrique inverse du robot, on va aborder dans le chapitre qui
suit l'étude cinématique qui va nous permettre de calculer ses
vitesses cartésiennes et articulaires.
| 


