à‰tude des différentes lois de commande pour un robot manipulateur à 6DDL comportant une liaison prismatique

II.4. le MGI du robot choisi

Le MGD du robot a été déjà établi au chapitre I, Les paramètres géométriques sont donnés dans Tableau I.1. .Puisque le robot a un poignet rotule (de centre O₄)on a utilisé la méthode de Paul avec découplage cinématique.

La position désirée de l'outil par rapport au repère atelier est donnée par la matrice :

On a calculé la matrice de transformationqui exprime le repèredans le repère suivant la relation:

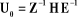
Le système d'équations qu'on doit résoudre est:

· Calcul de  :

Puisque, on peut écrire que la quatrième colonne deest égale à la quatrième colonne du produit des transformations  :

(II-12)

En prémultipliant l'équation précédente par , on obtient : pour les éléments de droite (la quatrième colonne de ):

(II-13)

En identifiant les éléments de l'équation en remarquant que : 

(II-14)

Cette équation est de type 2, elle admit les deux solutions suivantes pour :

(II-15)

En prémultipliant encore par , on obtient :

Par identification terme à terme de ce système d'équations on peut trouver et  ; la résolution de la première équation (équation de type 2) et après simplification, nous donne pourles solutions suivantes :

(II-16)

Connaissant, on peut calculer à partir de la deuxième équation (équation de type 1), la solution obtenu est : (II-17)

· Calcul de  :

Les variables étant connues, on s'intéresse maintenant aux équations d'orientation (II-11).

On note : (II-18)

où : est la matrice d'orientation de la matrice

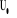
Les expressions de F, G et H s'écrivent :

(II-19-a)

(II-19-b)

(II-19-c)

A partir de l'équation (II-18) on a :

(II-20)

Les éléments de représentent les termes d'orientations de déjà calculés pour le MGD :

(II-21)

En prémultipliant cette équation par , on obtient :

(II-22)

(II-23)

A partir des éléments de (2,3) on obtient une équation de type 2 en, qui donne les deux solutions :

(II-24)

A partir des éléments de (1,3) et (2,3) on obtient un système d'équations de type 3 en, qui a pour solution :

(II-25)

Enfin, en considérant les éléments (2,1) et (2,2) on obtient un système d'équations de type 3 en, qui a comme solution :

(II-26)

Le nombre total de solutions pour le modèle géométrique inverse est égal à huit () : c'est à dire que l'outil de robot peut atteindre un point désiré de son espace opérationnel atteignable par huit configurations possibles.

Si on veut donner la position désirée en utilisant les angles de RTL, dans ce cas le MGI se fait en calculant d'abord les cosinus directeurs en fonction de ces angles , puis remplacer les valeurs trouvées dans les solutions calculées, sachant que :

(II-27)