Section 2 : Appréciation des facteurs
explicatifs de la rentabilité bancaire au Cameroun
L'estimation des facteurs explicatifs de la rentabilité
bancaire au Cameroun se fera par l'estimation de l'équation du rendement
des actifs. Mais avant l'estimation de ce modèle, notre attention
portera sur la trimestrialisation des données et la stabilité des
variables du modèle.
I - prolongement de la période et test de
normalité des variables du modèle
Par contrainte de la longueur de la période
d'étude, nous nous proposons d'accroître notre échantillon
en trimestrialisant les données. Cependant, il s'avère important
de présenter l'indice de Hirschman-Herfindal.
I 1 - présentation de l'indice de
Hirschman-Herfindal
Pour mesurer la diversification, nous utilisons l'indice de
Hirschman-Herfindahl. Cet indice est calculé comme la somme des
carrés de la fraction du poids d'un type de crédit sur le poids
total des crédits du portefeuille. On peut ainsi noter :
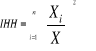
Où n est le nombre de différent type de
crédit d'un portefeuille de crédits et Xi mesure la
quantité de crédit i octroyée par le secteur bancaire.
Xi représente ainsi la quantité du crédit de
court terme, la quantité du crédit de moyen terme ou la
quantité du crédit de long terme. La plus petite et la plus
grande valeur possibles de l'indice de Hirschman-Herfindahl sont données
par 1/n = IHH et 1= IHH. Ainsi, en conclusion on aboutit
à la concentration du portefeuille de crédit sur un type de
crédit lorsque IHH est plus proche de un. Par contre, le
portefeuille est parfaitement diversifié lorsque IHH est
égale à 1/n.
L'indice de Hirschman-Herfindahl (IHH) peut
être aussi utilisé pour mesurer la concentration d'un
marché ou d'une entité dans un système. Il est égal
à la somme des carrés des parts de marché des entreprises
présentes sur le marché considéré. Pour son
interprétation, trois concepts sont habituellement retenues : le
marché à concentration faible, le marché moyennement
concentré et le marché à concentration
élevée. L'indice de Herfindahl-Hirschman est en effet fonction du
nombre d'entreprises présentes sur le marché, plus ce nombre
augmente, plus IHH diminue.
Dans notre cas, nous avons construit un indice de
Hirschman-Herfindahl pour la diversification du portefeuille de crédits
notée IHHP.
I 2 - trimestrialisation des données annuelles
et test de normalité
La période pour laquelle les données sont
disponibles étant relativement courte, la trimestrialisation des
données annuelles doit être menée afin d'accroître le
nombre d'observation. Nous recourons dans ce cadre à la formule
utilisée par Mansouri et Afroukh (2008). Pour chaque variable Z
annuellement observée, nous associons une quantité q
telle que:
 (1) avec (1) avec
Zt : la valeur à l'année courante,
Zt-1 : la valeur à l'année
antérieure,
Zt+1 : la valeur à l'année
ultérieure.
Les estimations des valeurs de la variable pour le premier
trimestre (T1), deuxième trimestre (T2),
troisième trimestre (T3) et quatrième trimestre
(T4) seront conduites comme suit:
T1 = 4[Zt/q].[(Zt-1) +
0,625Zt - 0,625(Zt-1)] (2)
T1 : la valeur au premier trimestre
T2 = 4[Zt/q].[(Zt-1) +
0,875Zt - 0,875(Zt-1)] (3)
T2 : la valeur au deuxième trimestre
T3 = 4[Zt/q].[Zt +
0,125(Zt+1) - 0,125Zt ] (4)
T3 : la valeur au troisième
trimestre
T4 = 4[Zt/q].[Zt +
0,375(Zt+1) - 0,375Zt ] (5)
T4 : la valeur au quatrième
trimestre
Au lieu de travailler sur une durée limitée
à neuf ans, il est possible de prolonger cette durée et avoir
324 observations soit (4 x 9 x 9). Autrement dit, la trimestrialisation nous
permettra de passer de neuf ans à 36 trimestres (4 x 9) et enfin
à 324 observations (36 x 9), ce qui correspond à la
multiplication du nombre de trimestres par le nombre des variables, les
trimestres variant de T1 :2000 à T4 :2008.
En ce qui concerne la normalité des termes d'erreur,
l'hypothèse de normalité de ces termes joue un rôle
essentiel car elle va préciser la distribution statistique des
estimateurs. C'est donc grâce à cette hypothèse que
l'inférence statistique peut se réaliser. L'hypothèse de
normalité peut être testée sur les variables du
modèle ou sur les termes d'erreur du modèle (Doucouré,
2005). Le test d'hypothèse est le suivant :
H0 : X suit une loi normale N(m, ó)
H1 : X ne suit pas une loi normale N(m,
ó)
La règle de décision est :
- On accepte l'hypothèse de normalité si la
statistique de Jarque-Bera est inférieure à 5,99.
- On rejette l'hypothèse de normalité si la
statistique de Jarque-Bera est supérieure à 5,99.
On peut aussi se baser sur la règle de décision
suivante :
- Au seuil de 5%, on accepte l'hypothèse de
normalité dès que la valeur de la probabilité est
supérieure à 0,05.
- Au seuil de 5%, on rejette l'hypothèse de
normalité dès que la valeur de la probabilité est
inférieure ou égale à 0,05.
En ce qui concerne notre étude, l'annexe numéro
2 résume le test de normalité des différentes variables.
De ce tableau, on constate que toutes les séries (ROA,
IHHP, KXACTF, FGACTF, LOGACTF,
INF, ACTFPIB, CONC, PIB,
Risk) suivent une loi normale sur la période
d'étude.
| 


