Chapitre 5 : Mise en place d'un logiciel de calcul de
la flèche d'un composite orthotrope et cas pratique
, y , , y ,
? 0
5.2.4.3. Champ de déplacement
cinématiquement admissible du système La plaque
étant sollicitée en flexion plane simple, il vient :
(5.3)
5.2.4.4. Expression du moment fléchissant
En effectuant une coupe fictive comme présentée
à la figure 5.53, nous avons l'équation d'équilibre
statique suivante :
(5.4)
Or : (5.5)
D'où : (5.6)
|
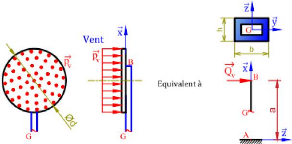
Figure 5.60 : Schéma
annoté d'un panneau de signalisation routière Application
à un panneau circulaire
Nous avons :
|
(5.7)
|
AN : (5.8)
(5.9)
Choix de la section : d'après le tableau
en annexe 5, la section encastrée correspond à la
section critique
et la valeur trouvée nous permet de choisir une poutre
à section rectangulaire type SD1, de
w x t ? ? D ? t
? x
0( , ) m cos m m
( )
. Cette poutre est réalisée sur nos route en
acier galvanisé.
5.2.4.5. Flèche maximale du système
? Pour le matériau homogène isotrope en
acier galvanisé
Pour un matériau homogène isotrope, le comportement
élastique est décrit par le module
d'Young et le coefficient de Poisson .
Ph
11 12(1 )
? v
Le coefficient de la matrice de rigidité en flexion est
:
(5.10)
( )2 2
m - 0.5 ?
Les résultats obtenus §2.2.3 deviennent : (5.11)
m
76
| 


