étude du comportement de la flèche d’un matériau composite en vibration et simulation sous Matlab.

4.3.2.2. Conditions aux limites : poutre encastrée à une extrémité et libre sur l'autre.

Nombre d'élément de base : ; Types d'éléments : STRI68

4.3.2.2.1. Résultats

? Présentation graphique des résultats

Mode1 : Mode 2 : Mode 3 :

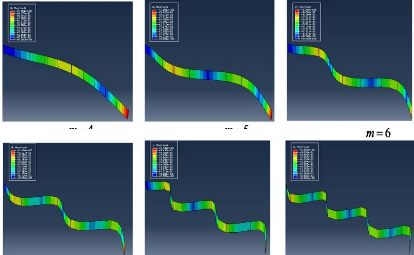
Mode 4 : Mode 5 : Mode 5 :

Figure 4.46 : Présentation graphique du comportement de la flèche sur une poutre EL

? Présentation numérique des résultats

Le tableau ci-dessous, établie la confrontation des résultats des flèches maximales obtenus au

cours du calcul par éléments finis à l'aide de ABAQUS avec ceux du code développé dans Matlab. Le but est de valider le code développé dans Matlab au moyen de l'erreur relative qui existe entre les deux méthodes.

Chapitre 4 : Simulation numérique sous Abaqus du comportement de la flèche d'une structure composite et validation du code

63

Tableau 4.23 : Comparaison des résultats obtenus par ABAQUS avec ceux du code développé.

	; ;
Modes	m	n	CODE (mm)	ABAQUS (mm)	Ecart (mm)	Ecart relatif i (%)
			EL	EL
1	1	1	1.5201	1.50153	-0.01857	-0.012
2	1	2	2.0369	1.99519	-0.04171	-0.021
	2	1	1.9984	1.84315	-0.155225	-0.084
3	2	3	2.0001	1.96815	-0.03195	-0.016
	3	2	2.0000	1.96009	-0.03991	-0.020
4	1	4	2.0000	1.96009	-0.03991	-0.020
	4	1	2.0000	1.96009	-0.03991	-0.020
5	1	5	2.0000	1.96009	-0.03991	-0.020
	5	1	2.0000	1.96009	-0.03991	-0.020

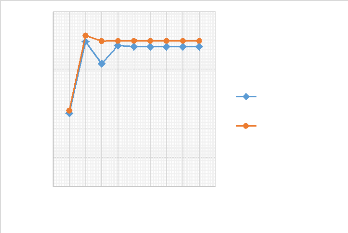
Le graphe ci-dessous rend plus visible l'écart relatif entre les deux résultats.

_ne ? ₃₀

W0max (mm)

2,2

1,8

1,6

1,4

1,2

2

1

0 1 2 3 4 5 6 7 8 9 10 Mode "m"

W0max ABAQUS (mm)

W0max CODE (mm)

_m ? ₁

Figure 4.47 : Présentation graphique du comportement de la flèche sur un pli orthotrope en appuis
simples sur ses 4 extrémités.

Cette représentation graphique nous montre dans le sens vertical la dispersion des deux

courbes. Cette dispersion est considérable entre le mode 2 et 3. La dispersion importante au mode

3 soit un écart relatif de 0,084.

4.3.2.2.2. Conditions aux limites : poutre en appuis simples sur ses deux extrémités.

Nombre d'élément de base : ; Types d'éléments : STRI68

4.3.2.2.3. Résultats

? Présentation graphique des résultats

Mode1 : Mode 2 : Mode 3 :

64

Chapitre 4 : Simulation numérique sous Abaqus du comportement de la flèche d'une structure composite et validation du code

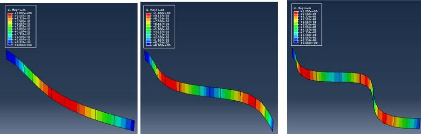
Mode 4 : Mode 5 : Mode 5 :

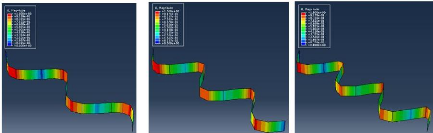
Figure 4.48 : Présentation graphique du comportement de la flèche sur une poutre EL 4.4. Validation du code de calcul

Les études faites au chapitre 2 montrent que la flèche est exprimée en fonction de la fréquence angulaire et du temps. Pour valider le code de calcul développé, il nous suffit de :

· Considérer les travaux de M. Assarar, A. El Mahi & J.-M. Berthelot ;

· Considérer les résultats des fréquences obtenus expérimentalement dans ces travaux ;

_h ? _{15 mm a} ? _{560 mm}

· Entrer les caractéristiques du même composite dans le code de calcul développé dans le cadre de cette recherche ;

· Extraire les résultats des fréquences ;

· Comparer les deux résultats ;

· Commenter la comparaison puis valider le code de calcul.

4.4.1. Présentation des travaux de M. Assarar, A. El Mahi & J.-M. Berthelot [13]