4.3.2. Comportement de la flèche des plaques par la
méthode des éléments finis et comparaison avec les
résultats du code développé.
4.3.2.1. Conditions aux limites : plaque en appuis
simples sur ses quatre côtés
Nombre d'élément de base : ; Types
d'éléments : STRI686
4.3.2.1.1.
Résultats
? Présentation graphique des
résultats
Mode1 : ; Mode 2 : ; ;
W 0 C ( Max )
W 0 A ( Max )
E w 0(max) ? w 0 A (
Max ) ? w 0 C (
Max )

59
Mode 3 : ; ; Mode 4 : ; ;
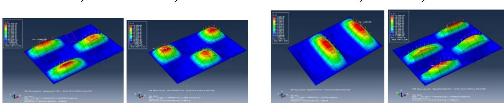
Figure 4.42: Présentation
graphique du comportement de la flèche sur un pli orthotrope
? Présentation numérique des
résultats
Le tableau ci-dessous, répertorie les
différentes valeurs des flèches maximales extraites dans le
calcul par éléments finis à l'aide de ABAQUS. Aussi, ces
résultats sont confrontés par ceux du code de calcul dans le but
de mettre en vue l'erreur relative qui existe entre les deux
méthodes.
Tableau 4.21 : Comparaison des
résultats obtenus par ABAQUS avec ceux du code
développé.
w ? w
0 A ( Max ) 0 C
( Max )
? 100
? x
w 0 A (
Max )
|
; ;
|
|
Modes
|
m
|
n
|
CODE (mm)
|
ABAQUS (mm)
|
Ecart (mm)
|
Ecart relatif i (%)
|
|
|
AAAA
|
AAAA
|
|
1
|
1
|
1
|
1.00060
|
1.06081
|
0.06021
|
5.67
|
|
2
|
1
|
2
|
1.00600
|
1.04100
|
0.035
|
3.36
|
|
2
|
1
|
1.00600
|
1.04100
|
0.035
|
3.36
|
|
3
|
2
|
3
|
1.00000
|
1.03208
|
0.03208
|
3.11
|
|
3
|
2
|
1.00000
|
1.03208
|
0.03208
|
3.11
|
|
4
|
1
|
4
|
1.00000
|
1.00000
|
0.000
|
0.00
|
6 STRI68 désigne le type d'élément
répondant aux hypothèses de Love-Kirchhoff
Chapitre 4 : Simulation
numérique sous Abaqus du comportement de la flèche d'une
structure composite et validation du code
60
|
4
|
1
|
1.00000
|
1.00000
|
0.000
|
0.00
|
|
5
|
1
|
5
|
1.00000
|
1.00000
|
0.000
|
0.00
|
|
5
|
1
|
1.00000
|
1.00000
|
0.000
|
0.00
|
Le graphe ci-dessous rend plus visible l'écart relatif
entre les deux résultats.
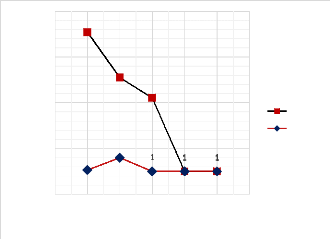
0 1 2 3 4 5 6
Modes
1,07
1,01
0,99
ABAQUS MATLAB
1,05
W0max
1,03
1,06081
1,041
1,03208
1,006
1,0006
Figure 4.43 : Présentation
graphique de l'écart relatif entre la flèche maximale
calculée par
MATLAB et celle calculée par ABAQUS.
Cette représentation graphique nous montre dans le sens
vertical la dispersion des deux courbes. Cette dispersion est
considérable pour les trois premiers modes d'excitations.
4.3.2.1.2. Explication du phénomène de
dispersion
Le phénomène de dispersion peut être
lié à une erreur du code de calcul développé ou une
erreur
de configuration des paramètres de maillage de la
structure. Cette dernière nous poussera à analyser l'influence du
nombre d'éléments (pas) sur le comportement de la flèche
d'une plaque.
4.3.2.1.3. Influence du nombre
d'éléments
Pour la même plaque, nous reprenons le test sous ABAQUS en
faisant varier le nombre d'éléments.
Tableau 4.22 : Comportement de la
flèche d'une plaque AAAA en fonction du nombre
d'éléments.
|
Modes
|
m
|
n
|
W0max ABAQUS (mm)
|
W0max
MATLAB
(mm)
|
|
5
éléments
|
20
éléments
|
30
éléments
|
80
éléments
|
100
éléments
|
1000
éléments
|
|
1
|
1
|
1
|
1.05092
|
1.13572
|
1.06081
|
1.00660
|
1.00010
|
1.000001
|
1.00060
|
|
2
|
1
|
2
|
1.14216
|
1.13804
|
1.04100
|
1.00440
|
1.00001
|
1.00000
|
1.00600
|
|
2
|
1
|
1.14216
|
1.13804
|
1.04100
|
1.00440
|
1.00001
|
1.00000
|
1.00600
|
|
3
|
2
|
3
|
1.13572
|
1.13572
|
1.03208
|
1.00208
|
1.00000
|
1.00000
|
1.00000
|
|
3
|
2
|
1.13572
|
1.13572
|
1.03208
|
1.00208
|
1.00000
|
1.00000
|
1.00000
|
|
4
|
1
|
4
|
1.13572
|
1.12100
|
1.00000
|
1.00000
|
1.00000
|
1.00000
|
1.00000
|
|
4
|
1
|
1.13572
|
1.12100
|
1.00000
|
1.00000
|
1.00000
|
1.00000
|
1.00000
|
Chapitre 4 : Simulation
numérique sous Abaqus du comportement de la flèche d'une
structure composite et validation du code
61
5
|
1
|
5
|
1.13572
|
1.12100
|
1.00000
|
1.00000
|
1.00000
|
1.00000
|
1.00000
|
|
5
|
1
|
1.13572
|
1.12100
|
1.00000
|
1.00000
|
1.00000
|
1.00000
|
1.00000
|
L'influence du type d'élément sur le comportement
de la flèche est explicitée par le graphe ci-dessous.
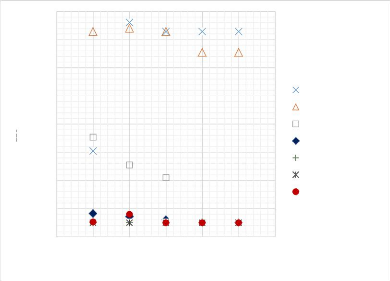
W0max
m ? 2 n ? 3
0,99
1,15
1,13
1,11
1,09
1,07
1,05
1,03
1,01
0 1 2 3 4 5 6
Modes
5 élts
20 élts 30 élts 80 élts 100
élts 1000 élts
W0max MATLAB
Figure 4.44 : Influence du
nombre d'éléments sur le comportement de la flèche d'une
plaque en appuis simples.
Effectivement, l'influence du nombre d'éléments
est considérable sur le comportement de la flèche. Donc, les
résultats deviennent acceptables à partir de 100
éléments comparativement au code de calcul
développé.
? Présentation graphique des résultats
pour un maillage de 100 éléments
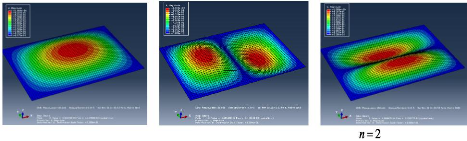
Mode 3 : ; ;
Mode 1 : ; Mode 2 : ; ;
Chapitre 4 : Simulation
numérique sous Abaqus du comportement de la flèche d'une
structure composite et validation du code

62
Figure 4.45 : Présentation
graphique du comportement de la flèche sur une plaque en
appuis
simples sur ses 4 extrémités.
| 


