3.3.2.4. Conclusion simulation des poutres
Donc, pour une application de poutres nécessitant une
minimisation de la flèche, il est
recommandé d'après cette analyse d'utiliser une
poutre de longueur supérieure à 200 mm, de hauteur
supérieure ou égale à 15 mm, avec un taux de
fibres supérieur ou égal à 35% de module d'Young
moyen supérieur ou égal à 8,5 GPa.
3.3.3. Modélisation des éléments
dans le cas d'une plaque en appuis simples Considérons une
plaque (pli orthotrope) rectangulaire constituée d'une matrice de
polyester et de
fibres de RC. Le pli est unidirectionnel et orienté
à 0°.
Mode 1 : m=1 ; n=1 Mode 2
: m=1 ; n=2 Mode 2 : m=2 ; n=1
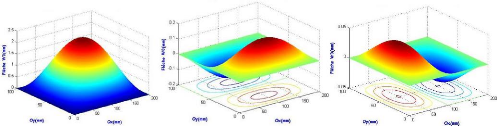
Chapitre 3 : Simulation numérique du comportement
vibratoire d'une structure composite
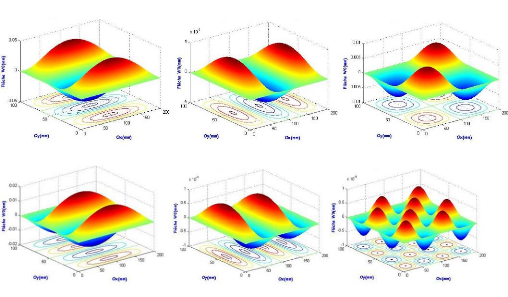
Mode 3 : m=1 ; n=3 Mode 3
: m=3 ; n=1 Mode 3 : m=2 ; n=2
Mode 4 : m=1 ; n=4 Mode 4
: m=4 ; n=1 Mode 4 : m=4 ; n=4
Mode 5 : m=1 ; n=5 Mode 5
: m=5 ; n=1 Mode 5 : m=5 ; n=5

51
Figure 3.37 : Comportement de la
flèche d'une plaque AAAA (pli à 0°) pour 5 modes.
Présentation numérique des
résultats
Ces résultats présentent les valeurs des
flèches maximales pour les différents modes. Tableau
3.19 : Valeurs des flèches maximales pour les 5
premiers modes d'une plaque AAAA
|
Em = 2, 8 GPa
|
Plaque rectangulaire 200x100x0,35 en
composite
Polyester/RC
|
Xf = 0.35
|
|
E = 8, 5 GPa
|
g0 = 100 N
|
|
Modes
|
1
|
2
|
3
|
4
|
5
|
|
m
|
1
|
1
|
2
|
1
|
3
|
1
|
4
|
1
|
5
|
|
n
|
1
|
2
|
1
|
3
|
1
|
4
|
1
|
5
|
1
|
|
Pli à 0°
|
|
W0Ma?? 2,314 0,17 0,042 0,0417 0,0041 0,016 8,33E-5
0,007 2,49E-5
|
|
Pli à 90°
|
|
W0Ma?? 0,4524 0,0032 0,1060 2,8E-4 0,0343 5,47E-4
0,0145 1,6E-4 0,0073
|
52
Chapitre 3 : Simulation numérique du comportement
vibratoire d'une structure composite
|
|
|
|
Stratifié [0/90]5
|
|
|
|
|
|
W0Max
|
0,032
|
0,0018
|
0,0018
|
4,25E-4 4,25E-4
|
1,62E-4
|
1,62E-4
|
7,87E-5
|
7,87E-5
|
|
|
|
|
Stratifié [0/90]5
|
|
|
|
|
|
W0Max
|
0,3991
|
0,0222
|
0,0222
|
0,0053 0,0053
|
0,0020
|
0,0020
|
9,78E-4
|
9,78E-4
|
Ces résultats montrent que le mode fondamental est le
plus dangereux. Car, la flèche est maximale pour ce mode. Les graphes
ci-dessous présentent le comportement de la flèche pour les
différentes structures.
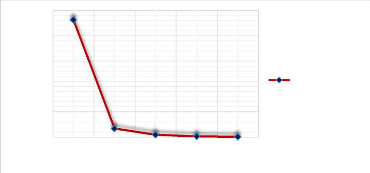
1 2 3 4 5
Modes
2,5
2
1,5
1
W0Max
0,5
0
2,314
0,17
0,047 0,016 0,007
w0max pli à 0°
Figure 3.38 : Comportement de la
flèche d'une plaque AAAA (pli à 0°) pour 5 modes.
Pour un pli à 0°, la flèche au mode 2 est
obtenue avec un pourcentage de chute de 92.65% sur le mode fondamental 1. Cette
flèche décroit et converge avec les modes.
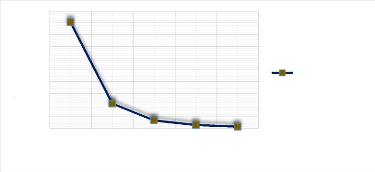
W0Max
0,45
0,35
0,25
0,15
0,05
0,5
0,4
0,3
0,2
0,1
0
0,4524
1 2 3 4 5
Modes
0,106
0,0343
0,0145
0,0073
w0max pli à 90°
Figure 3.39 : Comportement de la
flèche d'une plaque AAAA (pli à 90°) pour 5 modes.
Pour un pli à 90°, la flèche au mode 2 est
obtenue avec un pourcentage de chute de 76.57% sur le mode fondamental 1. Cette
flèche décroit et converge avec les modes.
53
Chapitre 3 : Simulation numérique du comportement
vibratoire d'une structure composite
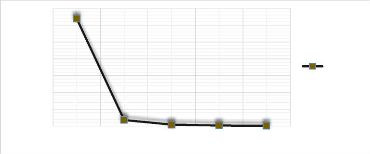
W0Max
0,035
0,025
0,015
0,005
0,03
0,02
0,01
0
0,032
1 2 3 4 5
Modes
0,0018
4,25E-04 1,62E-04
7,87E-05
w0max
stratifié
[0/90]s
Figure 3.40 : Comportement de la
flèche d'une plaque AAAA (stratifié symétrique à
[0/90]s) pour 5 modes. Pour un stratifié
symétrique à [0/90]s, la flèche au mode 2 est
obtenue avec un pourcentage de chute de 94.375% sur le mode fondamental 1.
Cette flèche décroit et converge avec les modes.
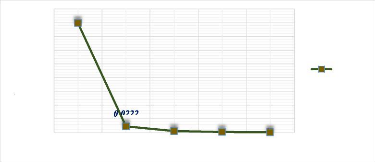
W0Max
0,45
0,35
0,25
0,15
0,05
0,4
0,3
0,2
0,1
0
0,3991
1 2 3 4 5
Modes
0
02
,
0,002 9,78E-04
w0max stratifié...
Figure 3.41 : Comportement de la
flèche d'une plaque AAAA (stratifié antisymétrique
à [0/90]s) pour les 5
premiers modes.
Pour un stratifié antisymétrique à
[0/90]s, la flèche au mode 2 est obtenue avec un pourcentage
de chute de 94.44% sur le mode fondamental 1. Cette flèche
décroit et converge avec les modes.
En définitive, les objectifs que nous poursuivons dans
ce chapitre ont été atteint, à savoir visualiser et
analyser le comportement des éléments de structures (plaques et
poutres). L'implémentation des équations sous Matlab nous a
fourni des résultats acceptables, car pour chaque élément
testé, les conditions aux limites étaient respectées au
préalable. Il a été constaté que les
paramètres comme la longueur, la hauteur, le taux de renforcement et le
module d'Young des fibres influencent raisonnablement sur le comportement de la
flèche au cours des vibrations transversales libres pour une structure
sollicitée en flexion et configurée sous diverses conditions aux
limites essentiellement. Aussi, nous avons constaté que ces
caractéristiques influencent sur la fréquence angulaire propre et
la période des oscillations. Les résultats obtenus restent
à être valider soit par une confrontation avec des
résultats expérimentaux, soit par confrontation avec les
résultats de la méthode des éléments finis ou par
confrontation des résultats d'un test expérimental tiré de
la littérature. Ces deux derniers process de validation seront
développés dans le chapitre 4.
CHAPITRE 4 : SIMULATION NUMERIQUE SOUS ABAQUS DU
COMPORTEMENT DE LA FLECHE D'UNE STRUCTURE COMPOSITE ET VALIDATION DU CODE DE
CALCUL
|
|



