Chapitre 1 : Etat de l'art sur le comportement
vibratoire d'un matériau composite
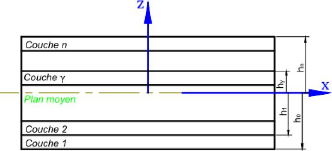
Figure 1.5 : Schéma d'un
stratifié à n couches
k=1 ?
Avec :
- : Représentent les coefficients de
rigidité en membrane d'expression :
(1.30)
- : Représentent les coefficients de
couplage membrane-flexion-torsion d'expression :
(1.31)
- : Représentent les coefficients de
rigidité en flexion d'expression :
|
n2 hk
D?? ? (Q l ao
/k[hkzk
? 12
|
a,f =1,3,6 (1.31)
|
Avec : sont les coefficients de rigidité réduit, et
sont respectivement la côte et
l'épaisseur de la couche ?? de n couches
mesurée à partir du plan moyen.
1.3.6. Equation constitutive générale d'un
stratifié en l'absence du cisaillement
Elle permet de lier les résultantes et les moments en
fonction des différentes déformations. Pour cela, il suffit
d'assembler (1.25) et (1.28) :
|
N 1 ?A11 A12 A16
B11 B12 B16 1 £
0
xx ?
? ? ? ? ?
0
? ? ?
N A A A B B B £
yy 12 22 26 12 22 26 ?
yy
? ? ?
? ? ?0
Nxy ? A16 A26 A66
B16 B26 B66 £xy
M?B11 B12 B16
D11 D12 D16 kxx ? ??
Myy? ?B12 B22 B26 D12
D22 D16 kyy
? ? ? ? ?
?M y J B16 B26
B66 D16 D16 D66 ????kxy J
|
(1.32)
|
Du point de vue de l'équation constitutive, un composite
est orthotrope si :
· Il n'existe aucun couplage membrane-flexion-torsion :
[B ] = [ 0] ;
· Il n'existe pas de couplage traction-cisaillement et
flexion-torsion : A16 = A26 = 0 et
D16=D16=0; (1.33)
| 


