Les retombées de la tertiarisation sur la croissance économique de la rdc

1.2 Traitement des données

Il importe de rappeler à ce niveau que, le traitement de données de notre étude est fait à l'aide du logiciel statistique de traitement des donnéesEviews 8.

En effet, notre analyse repose sur l'écriture d'un modèle reliant le Produit intérieur brut (PIB) à la production du secteur Tertiaire (TERT). Il s'agit d'étudier la relation existante entre le secteur tertiaire et la croissance économique de la R.D.C et voir dans quelle mesure le secteur tertiaire influence la croissance économique.

La formulation de l'équation du modèle à estimer est la suivante :

PIB= f (TERT).

L'équation du modèle de départ que nous allons estimer s'écrit comme suit :

PIB = a₀ + a₁TERT + _i

Avec :

PIB: la variable dépendante (expliquée)

TERT : la variable indépendante (explicative)

a_i : Les coefficients à estimer

_i: le terme d'erreur.

1. Estimation du modèle

Il existe trois raisons principales pour construire et estimer des modèles économétriques. Premièrement on étudie les relations et les dépendances entre les variables macro-économiques ; deuxièmement, on cherche la possibilité les effets des variations des variables indépendantes particulières sur les variables endogènes du modèle en faisant des simulations ; troisièmement, on utilise le modèle pour faire dans le future, une prévision de l'évolution économique.

Dans notre étude, c'est le deux premiers aspects qui nous intéresse beaucoup plus, il s'agit d'étudier les relations existantes entre le secteur tertiaire et la croissance économique mais également nous cherchons à déterminer les effets de la tertiarisation sur la croissance économique.

Tableau n°3 : tableau relatif à l'estimation du modèle

DependentVariable: PIB
Method: Least Squares
Date: 12/01/20 Time: 12:45
Sample: 1989 2018
Includedobservations: 30
Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	9360.317	163182.8	0.057361	0.9547
TERT	2.914119	0.022138	131.6339	0.0000
R-squared	0.998387	Meandependent var		11961669
Adjusted R-squared	0.998329	S.D. dependent var		18167721
S.E. of regression	742644.9	Akaike info criterion		29.93816
Sumsquaredresid	1.54E+13	Schwarz criterion		30.03158
Log likelihood	-447.0725	Hannan-Quinn criter.		29.96805
F-statistic	17327.48	Durbin-Watson stat		1.358208
Prob(F-statistic)	0.000000

Source : sortie Eviews 8

L'équation obtenue est : PIB = 9360,32 + 2,91 TERT

(0,06) (131,63)

(.) : Ratio de student

- Le modèle est explicatif à 99,8% (R² = 0,998387),ceci veut dire que pour ce modèle, le Produit intérieur brut est expliqué à 99,8% par le secteur tertiaire et à 0,2% par d'autres facteurs non pris en compte dans le modèle.

Mais cela ne veut pas dire que la proportion du secteur tertiaire dans le produit intérieur brut est de 99,8% et que celle de deux autres secteurs est de 0,2%.

L'incidence du secteurtertiaire sur le PIB est très élevée car R² est voisin de 100%.

La variable endogène et la variable exogène évoluent dans le même sens, car la pente de la droite est positive.

Dans le cas sous examen, lorsque la variable exogène augmente d'une unité, la variable endogène augmente de 2,91 unités.

Ce résultat nous permet d'affirmer notre hypothèse selon laquelle, la tertiarisation influence de manière positive la croissance économique de la R.D.C car, plus le tertiaire est élevé, plus la croissance l'est aussi et vice-versa.

2. Calcul du coefficient de corrélation

Le coefficient de corrélation r = 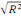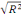permet de déterminer le sens et l'intensité de la liaison entre les deux variables. Nous allons l'interpréter par rapport au signe et par rapport au degré de liaison entre variables.

Son interprétation est contenue dans le tableau ci-dessous :

Tableau n°4 : Tableau relatif à l'interprétation du coefficient de corrélation

A. Interprétation par rapport au signe	§ Si rXY> 0, X et Y sont positivement corrélées [les deux variables évoluent dans le même sens]. § Si rXY< 0, X et Y sont négativement corrélées [les deux variables évoluent dans un sens opposé]. § Si rXY = 0, X et Y sont non corrélées [c-à-d qu'il n'existe pas de liaison linéaire entre les deux variables].
B. Interprétation par rapport à l'intensité	§ Si rXY = #177; 1 (100 %), le lien linéaire entre X et Y est parfait. § Si 0.80 <rXY< 1, le lien linéaire est très fort. § Si 0.65 <rXY< 0.80, le lien linéaire est fort [élevé]. § Si 0.50 <rXY< 0.65, le lien linéaire est modéré. § Si 0.25 <rXY< 0.50, le lien linéaire est faible. § Si 0.025 <rXY< 0.25, le lien linéaire est très faible.

Source : [Kapinga J. (2019)]

Dans le cas sous examen r = 0,9992et s'interprète comme suit :

- Par rapport au signe : il est positif, cela signifie que les deux variables sont positivement corrélées c'est-à-dire qu'elles évoluent dans la même direction (l'augmentation de la variable exogène entraîne l'augmentation de la variable endogène)

- Par rapport à l'intensité de la liaison : il est presque égal à 1 ou 100%; donc le lien linéaire entre les deux variables est parfait.

Ainsi donc, le coefficient de corrélation nous permet également d'affirmer l'hypothèse selon laquelle il existe une relation parfaite entre le tertiaire et la croissance économique étant donné que r= 0,9992 et que l'intensité de la liaison est presqu'égal à 1.

3. Test global du modèle

Il permet de vérifier si le modèle est globalement significatif.

- Hypothèses : deux hypothèses peuvent être émises :

- H₀ : le modèle n'est pas significatif

- H₁ : le modèle est significatif

- Règle de décision : On rejette H₀ lorsque la probabilité associée à F-statistic est inférieure à 0,05 (5%)

La lecture du tableau ci-haut (tableau relatif à l'estimation du modèle) témoigne que le modèle est globalement significatif car la probabilité associée à F-statistic(0.0000)estinférieure à(0,05) 5%, on rejette donc l'Hypothèse nulle H₀.

4. Tests individuels des paramètres

Ici nous nous intéressons à la significativité individuelle des paramètres a₀ et a₁

- Hypothèses : deux hypothèses peuvent être émises :

- H₀ : le paramètre n'est pas significatif

- H₁ : le paramètre est significatif

- Règle de décision : On rejette H₀ lorsque la probabilité associée à t-statistic est inférieure à 0,05 (5%)

· Test du paramètre « a₀ »

La valeur de la probabilité associée à t-statistic(0,9547) étant supérieure à 0,05 (5%), nous acceptons l'hypothèse nulle H₀, donc le paramètre « a₀ » n'est pas significatif dans le modèle.

La non significativité de l'ordonnée à l'origine n'a pas d'incidence sur le modèle, car ce qui importe plus c'est la significativité de la pente de la droite.

· Test du paramètre « a₁ »

La valeur de la probabilité associée à t-statistic(0,0000) étant inférieure à 0,05 (5%), nous rejetons l'hypothèse nulle H₀, donc le paramètre « a₁ » est significatif dans le modèle.

5. Test de normalité des résidus.

En statistiques, les tests de normalité permettent de vérifier si des données réelles suivent une loi normale ou non.

Pour tester la normalité des résidus, nous utilisons le « test de JarqueBera » dont les résultats seront donnés dans le tableau ci-dessous :

- Hypothèses : deux hypothèses peuvent être émises :

- H₀ : lesrésidus sont normalement distribués

- H₁ : les résidus ne sont pasnormalement distribués

- Règle de décision : On rejette H₀ lorsque la probabilité associée à la statistique de JarqueBera est inférieure à 0,05 (5%).

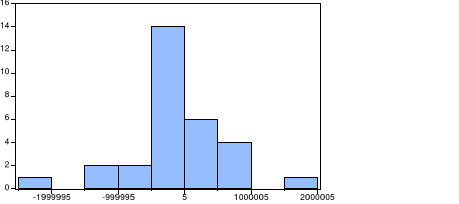
Figure n°3 : Test de normalité de JarqueBera

Source : Résultat du traitement à partir du logiciel Eviews 8

La probabilité associée à la statistique de JarqueBera(0,001585) étant inférieure au seuil statistique de 0,05 (5%), nous rejetons H₀, nous considérons que les résidus ne sont pas normalement distribués.

6. Test d'autocorrélation des erreurs

- Hypothèses : deux hypothèses peuvent être émises :

- H₀ : il y a absence d'autocorrélation des erreurs

- H₁ :il y a autocorrélation des erreurs

- Règle de décision : On rejette H₀ lorsque la Prob(Obs*R-squared)est inférieure à 0,05 (5%).

Tableau n°5 : Tableau relatif au test d'autocorrélation des erreurs

Breusch-Godfrey Serial Correlation LM Test:
F-statistic	2.713190	Prob. F(2,26)		0.0851
Obs*R-squared	5.180088	Prob. Chi-Square(2)		0.0750
Test Equation:
DependentVariable: RESID
Method: Least Squares
Date: 12/02/20 Time: 14:06
Sample: 1989 2018
Includedobservations: 30
Presamplemissing value laggedresiduals set to zero.
Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	11480.95	159612.9	0.071930	0.9432
TERT	-0.000909	0.025323	-0.035907	0.9716
RESID(-1)	0.421802	0.239623	1.760273	0.0901
RESID(-2)	-0.447277	0.243240	-1.838831	0.0774
R-squared	0.172670	Meandependent var		-1.23E-09
Adjusted R-squared	0.077208	S.D. dependent var		729728.3
S.E. of regression	700991.9	Akaike info criterion		29.88195
Sumsquaredresid	1.28E+13	Schwarz criterion		30.06877
Log likelihood	-444.2292	Hannan-Quinn criter.		29.94171
F-statistic	1.808793	Durbin-Watson stat		1.746648
Prob(F-statistic)	0.170330

Source : Résultat du traitement à partir du logiciel Eviews 8

De ce tableau, nous remarquons qu'il n'y a pas d'autocorrélation des erreurs car la Prob (Obs*R-squared) est supérieure à 5%, donc nous acceptons l'hypothèse nulle.

7. Test d'hétéroscédasticité
Hypothèses : deux hypothèses peuvent être émises :

· H₀ : il y a Homoscédasticité

· H₁ : il y a Hétéroscédasticité

§ Règle de décision : On rejette H₀ lorsque la Prob(Obs*R-squared) est inférieure à 0,05 (5%).

Tableau n°6 : Tableau relatif au test d'hétéroscédasticité

HeteroskedasticityTest:Breusch-Pagan-Godfrey
F-statistic	11.24058	Prob. F(1,28)		0.0023
Obs*R-squared	8.593588	Prob. Chi-Square(1)		0.0734
Scaledexplained SS	18.55914	Prob. Chi-Square(1)		0.0000
Test Equation:
DependentVariable: RESID^2
Method: Least Squares
Date: 12/02/20 Time: 15:40
Sample: 1989 2018
Includedobservations: 30
Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	1.04E+11	2.20E+11	0.471921	0.6406
TERT	100164.7	29875.86	3.352697	0.0023
R-squared	0.286453	Meandependent var		5.15E+11
Adjusted R-squared	0.260969	S.D. dependent var		1.17E+12
S.E. of regression	1.00E+12	Akaike info criterion		58.16869
Sumsquaredresid	2.81E+25	Schwarz criterion		58.26210
Log likelihood	-870.5303	Hannan-Quinn criter.		58.19857
F-statistic	11.24058	Durbin-Watson stat		1.818000
Prob(F-statistic)	0.002307

Source : Résultat du traitement à partir du logiciel Eviews 8

La probabilité associée à Obs*R-squared est supérieure à 5 %, donc il y a absenced'hétéroscédasticité (c'est-à-dire Homoscédasticité).