Les retombées de la tertiarisation sur la croissance économique de la rdc

2.2 Le modèle de régression avec un prédicteur : la variable X

Le but d'un modèle est d'expliquer le mieux possible la variabilité de la variable dépendante (y) à l'aide d'une ou plusieurs variables indépendantes (x). Dans le cas de la régression linéaire simple, le modèle ne contient qu'une seule variable indépendante.

Il est très important de comprendre que pour être valable, un modèle avec prédicteur doit expliquer significativement plus de variance qu'un modèle sans prédicteur. Sinon, on est encore mieux avec seulement la moyenne. La première chose à faire dans l'interprétation des résultats sera donc de vérifier si le modèle de régression avec prédicteur (notre variable x) sera significativement plus intéressant qu'un modèle sans prédicteur (la moyenne de y).

1. Aspect algébrique du modèle de régression: Équation de la droite de régression linéaire simple

Le modèle de régression peut aussi se représenter sous une forme mathématique. En fait, la droite de régression s'exprime avec l'équation algébrique décrivant une droite dans un plan cartésien. Si y est la variable placée sur l'axe vertical (ordonnée) et x, la variable placée sur l'axe horizontal (abscisse), l'équation est :

Y_prédit = b_o + b₁X

Le coefficient b₀ est appelée l'ordonnée à l'origine ( ou constante). C'est la valeur prédite de y quand x = 0. 

Le coefficient b₁ est appelé la pente. C'est le changement sur y lorsque x change d'une unité.

Y est généralement appelé variable dépendante (dans la mesure où nous tentons d'expliquer la variabilité de y avec les valeurs de la variable x) et x est généralement appelé variable indépendante.

Dans notre exemple, la variable dépendante est la croissance économique et la variable indépendante est la production du secteur tertiaire. Nous tentons donc d'expliquer la variabilité de la croissance économique mesurée par le PIB en fonction des activités du secteur tertiaire.

2. Évaluation de la qualité d'ajustement du modèle de régression avec prédicteur : R² et R

Nous venons de voir l'amélioration de l'explication de la variabilité de la croissance économique en partant du modèle le plus simple (seulement la moyenne) jusqu'à l'ajout de la variable indépendante, qui nous a permis de réduire de beaucoup les résiduels entre la droite et les observations.

En effet, il s'agit de savoir si la variable que nous mettons en relation avec la variable dépendante permet de mieux expliquer sa variabilité, donc de diminuer de manière significative les résiduels calculés dans un modèle sans prédicteur ?

Elle représente la différence entre le modèle sans prédicteur et celui avec un prédicteur et s'appelle somme des carrés du MODÈLE (SC_M). C'est en fait la soustraction entre SC_T (variation totale) et SC_R (résiduel).

Lorsque cette somme est très différente de la somme totale, l'ajout de la variable a grandement amélioré le modèle. Une somme plus modeste indiquerait que l'ajout de cette variable indépendante n'a pas permis de mieux expliquer la variabilité de y. 

La manière de représenter cette amélioration est de faire le rapport entre la somme des carrés du modèle avec prédicteur (SC_M) et la somme des carrés du modèle sans prédicteur (SC_T).

Le résultat de ce rapport est appelé R² et sert à exprimer en pourcentage (lorsque multiplié par 100) la proportion de variance de y qui est expliquée par le modèle (SC_M) par rapport à la quantité de variance qu'il y avait à expliquer au départ (SC_T).

 

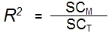
Nous verrons plus loin que la racine carrée de R² dans le cadre de la régression simple donne le coefficient de corrélation (R) et que celui-ci est un bon estimateur du degré global d'ajustement du modèle. 

La valeur F

Les types de somme des carrés servent aussi à calculer l'ajustement du modèle avec le test de la valeur F. 

La régression est basée sur le rapport entre le carré moyen de l'amélioration due au modèle (SC_M) et le carré moyen de la différence observée entre le modèle et les données réelles (SC_R). 

Pour le carré moyen du modèle (CM_M), on divise le SC_M par le nombre de variable dans le modèle (ici 1) et pour le carré moyen résiduel (CM_R), on divise la SC_R  par le nombre de sujets moins le nombre de paramètres « b » estimés (ici b₀ et b₁). 

Au final, il faut comprendre que la valeur F est une mesure de combien le modèle s'est amélioré dans la prédiction de y comparativement au degré d'imprécision du modèle.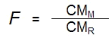 

Si un modèle est bon, l'amélioration de la prédiction due au modèle devrait être grande (CM_M sera élevé) et les différences entre le modèle (droite de régression) et les valeurs observées, petites (CM_R devrait être faible). 

3. Évaluation de l'ajustement de la droite de régression aux données

La droite de régression des moindres carrés est la ligne qui résume le mieux les données dans le sens où elle possède la plus petite somme des carrés des résiduels. Ceci dit, cela ne signifie pas nécessairement que cette droite est bien ajustée aux données. Donc, avant d'utiliser la droite de régression pour prédire ou décrire la relation entre deux variables, on doit donc vérifier la qualité d'ajustement de la droite avec les données avec la valeur de R, soit le coefficient de corrélation. Si la droite est peu ajustée aux données, les conclusions basées sur celle-ci seront imprécises voire invalides. 

4. Estimation de la variabilité expliquée par le modèle

En dernier lieu, il faut évaluer la proportion de la variabilité totale qui est expliquée par le modèle de régression. Pour ce faire, on utilise les valeurs des sommes des carrés.

En fait, la modélisation par régression tient en trois éléments interreliés qui se trouvent invariablement dans tous les modèles de régression simple ou multiple :

La variabilité totale(SC_T) : C'est la variance de la variable dépendante que nous cherchons à expliquer (sans aucun prédicteur

La variabilité expliquée par le modèle (SC_M) : C'est la partie de la variance totale qui est expliquée par l'ajout d'un prédicteur, c'est-à-dire la construction d'un modèle.

La variabilité non expliquée par le modèle (SC_R) : C'est la partie de la variance qui n'est pas expliquée par le modèle et qui reste donc à expliquer avec d'autres variables indépendantes.

De ces éléments, on tire deux informations fondamentales en régression, soit :

1) La proportion de variance expliquée par le modèle

 

Plus la proportion est élevée, plus le modèle est puissant. L'inverse est aussi vrai.

2) La proportion de variance non expliquée par le modèle (variance résiduelle)