Section 2 : La
démarche empirique
2.1 Etude de
corrélation
Le test de corrélation (contrairement à la
régression simple) ne propose pas d'identifier une variable
dépendante et une variable indépendante. On ne cherche
qu'à déterminer l'absence ou la présence d'une relation
linéaire significative entre les variables.
Par exemple, nous pouvons être intéressés
à savoir si le secteur tertiaire est associé à la
croissance économique.
Ces variables peuvent être :
- Associées positivement (r > 0) : plus le nombre
d'heures d'étude augmente, plus le rendement augmente;
- Associées négativement (r < 0) : plus le
nombre d'heures d'étude augmente, plus le rendement diminue;
- Non associées (r = 0) : le nombre d'heures
d'études n'a aucune influence sur le rendement.
La corrélation est une quantification de la relation
linéaire entre des variables continues. Le calcul du coefficient de
corrélation de Pearson repose sur le calcul de la covariance entre deux
variables continues. Le coefficient de corrélation est en fait la
standardisation de la covariance. Cette standardisation permet d'obtenir une
valeur qui variera toujours entre -1 et +1, peu importe l'échelle de
mesure des variables mises en relation.
· L'hypothèse nulle est donc que les deux
variables ne sont pas associées, qu'il n'y a pas de relation entre ces
dernières (r = 0).
· L'hypothèse alternative est qu'il existe une
relation linéaire entre les deux variables.
Pour bien comprendre le calcul du coefficient de
corrélation, il est nécessaire de revenir sur le concept de
covariance.
Quand des variables covarient, un écart à la
moyenne d'une variable est accompagné par un écart dans le
même sens ou dans le sens opposé de l'autre pour le même
sujet. Donc, pour chaque valeur qui s'écarte de la moyenne, on
s'attend à trouver un écart à la moyenne pour l'autre
variable.
M Pearson a eu la brillante idée de faire en sorte que
toutes les données soient comparées à partir d'une
unité de mesure en laquelle toutes les échelles de mesures
peuvent être converties : l'écart-type.
Nous nous rappelons que l'écart-type, comme la
variance, est une mesure de la dispersion des données autour de la
moyenne. Lorsque nous divisons n'importe quelle distance de la moyenne par
l'écart-type, nous obtenons cette distance en unités
d'écart-type.
Nous pouvons donc suivre la même logique pour trouver la
covariance en unités d'écart-type. Il faut toutefois se rappeler
que puisque nous avons deux variables, nous avons aussi deux écart-
types.
Puisque nous allonscalculer la variance pour chaque variable
avant de les multiplier, nous allons en faire de même avec les
écart-types : nous les multiplions et divisons la sommation de la
multiplication des deux variances par le produit des deux
écart-types.
Nous obtenons ainsi le coefficient de corrélation de
Pearson [R. Rico, (2006)] :
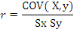
Pour être interprété, le coefficient de
corrélation doit être significatif (la valeur de p doit être
plus petite que 0,05). Si le coefficient est non significatif, on
considère qu'il est semblable à r = 0. Par contre, lorsqu'il est
significatif, le coefficient de corrélation donne deux informations
importantes :
- Le sens de la relation linéaire entre les deux
variables : Le coefficient de corrélation, qui présente
finalement la covariance standardisée, varie entre - 1 et 1. Un
coefficient de 1 indique une corrélation positive parfaite entre les
deux variables. À l'inverse, un coefficient de - 1 indique une
corrélation négative parfaite: lorsque la variable x augmente, la
variable y diminue dans la même proportion. Dans les deux cas, les points
tombent parfaitement sur la droite. Un coefficient de 0 indique qu'il n'y a
aucune relation entre les deux variables. Ainsi, la variation de l'une n'est
aucunement associée à la variation de l'autre.
- La force de la relation linéaire entre les deux
variables : Plus la valeur du coefficient est proche de + 1 ou de -
1, plus les deux variables sont associées fortement. Au contraire, plus
le coefficient est près de 0, moins les variables partagent de
covariance et donc, moins l'association est forte. On peut qualifier la force
de cette relation avec les balises de Cohen concernant la taille
d'effet.
Pour la corrélation, nous n'avons pas à
effectuer de calcul particulier pour connaître la taille d'effet. Nous
regardons seulement la valeur du coefficient et nous l'interprétons
selon les balises de Cohen (1988) [R. Rico, (2006)] :
Autour de 0,10 effet de petite taille
corrélation faible
Autour de 0,30 effet de taille moyenne corrélation
moyenne
Autour de 0,50 effet de grande taille
corrélation forte
Les questions auxquelles répond la modélisation
de la relation linéaire dans le cas de notre étude sont celles-
ci :
Quel est l'effet de la tertiarisation ou de la
prépondérance des activités du secteur tertiaire sur la
croissance économique en RDC ?
Existe-t-il une corrélation entre les
activités du secteur tertiaire et la croissance
économique ?
Nous allons étudier la plus simple des
modélisations: la régression linéaire simple.
Hypothèse nulle
Dans le cas de la régression, l'hypothèse nulle
est qu'il n'y a pas de relation entre la variable dépendante et la
variable indépendante, donc que la variable indépendante ne
permet pas de prédire la variable dépendante.
L'hypothèse alternative est qu'il est possible de
prédire la variable dépendante à partir de la variable
indépendante.
Prémisses
1. Distribution
normale : les valeurs de la variable dépendante sont
normalement distribuées.
2. Homogénéité
des variances : la variance dans la distribution de la variable
dépendante doit être constante pour toutes les valeurs de la
variable indépendante.
3. Le prédicteur (la
variable indépendante) doit présenter une certaine
variance dans les données (pas de variance nulle).
4. Le prédicteur n'est pas
corrélé à des variables externes (qui n'ont
pas été intégrées au modèle) qui influencent
la variable dépendante.
5. Homoscédasticité :
pour toutes les valeurs du prédicteur, la variance des résiduels
(erreur de mesure) est homogène. Cette prémisse peut être
vérifiée par l'examen du nuage de points du croisement entre les
valeurs prédites standardisées et les résiduels
standardisés.
6. Distribution normale
et aléatoire des résiduels : cette prémisse
signifie que la différence entre le modèle et les valeurs
observées sont près de zéro. Elle peut être
vérifiée par l'examen du nuage de points qui a servi à
vérifier la prémisse d'homoscédasticité.
7. Les valeurs de
la variable
dépendante sont indépendantes : chaque
valeur de la variable dépendante vient d'une observation distincte. Les
observations ne sont pas reliées entre elles.
8. Relation linéaire
entre la variable indépendante et la variable
dépendante : la relation modélisée est
linéaire. Cette prémisse peut être vérifiée
par le nuage de points du croisement entre ces deux variables.
| 


