2.4.1.5 Normalisation du
graphe
Si le graphe doit débuter par plusieurs Tâches
simultanées, il ne doit y avoir qu'une seule étape
d'entrée (ou étape de début, ou étape de
départ). Les étapes seront donc regroupées en une
seule.
Illustrons cela :
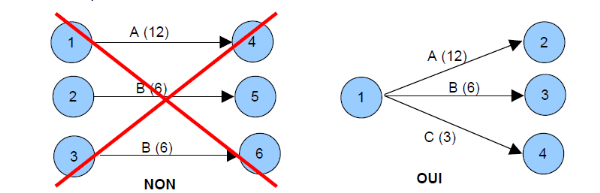
Figure 2.7 : Normalisation du graphe
Pert
Si le graphe se termine par plusieurs Tâches (plusieurs
étapes de sortie (ou de fin), il ne doit y avoir qu'une seule
étape de sortie.
Autre Problème de
dépendance
Si nous avons par exemple le cas suivant : A enclenche
B, A enclenche D, C enclenche D. Nous pouvons être tentes de dessiner le
graphe de la manière suivante :
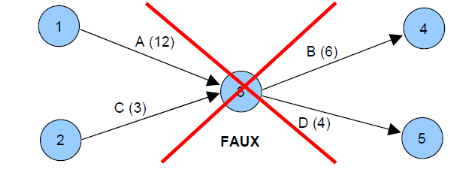
Figure 2.8 : Normalisation du graphe
Pert
Le graphe précédent je précise est faux
car cette construction signifie : A enclenche B, A enclenche D, C enclenche B,
et C enclenche D. Dans le souci de respecter les contraintes
d'antériorités de notre projet, nous pouvons améliorer le
graphe précédent en introduisant une Tâchefictive, Ce qui
nous conduit a :
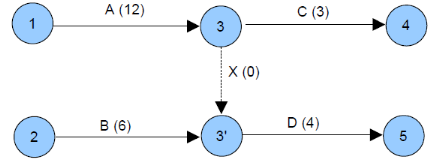
Figure 2.9 : Normalisation du graphe
Pert
La méthode PERT permet de résoudre le
problème central d'ordonnancement par le graphe PERT. Dans ce travail,
Il ne sera considéré que les graphes PERT temps
c'est-à-dire graphe PERT temps déterministe.
2.4.1.6
Représentation des étapes
Les étapes ou noeuds dans le graphe PERT peuvent
être représentés de différentes façons selon
les informations que l'on souhaite mettre en évidence.
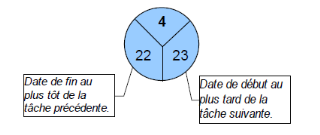
Figure 2.10 : Composition d'une étape dans
le graphe Pert
2.4.1.7
Méthodologie de construction d'un réseau PERT (Graphe PERT)
Pour construire un réseau PERT, Il faudrait au
préalable :
ü Etablir la liste des Tâches (faire le
partitionnement des Tâches en fonction des ressources), Ou bien
établir le dictionnaire de précédent qui sera un atout
majeur dans la suite.
ü Déterminer des antériorités :
Tâches immédiatement antérieures, et Tâches
antérieures.
La notion de niveau (Utilisé dans la construction du
graphe potentiel) n'a pas de sens pour la méthode PERT car les
tâches sont représentées par les arcs dans la
méthode PERT.
ü Construire le réseau PERT.
Calculer la durée du projet, les dates début et
de fin des Tâches.
Déterminer le chemin critique.
Un chemin est dit critique si celui-ci passe par des
étapes dont les dates au plus tôt et les dates au plus tard
sont égales pour chaque étape
Voici un exemple pratique du graphe PERT
|
Tâches
|
Antériorités
|
Durées
|
|
A
|
|
1
|
|
B
|
|
2
|
|
C
|
A
|
1
|
|
D
|
|
3
|
|
E
|
B
|
2
|
|
F
|
E
|
5
|
|
G
|
C ,D
|
2
|
|
H
|
|
5
|
|
I
|
H
|
2
|
|
J
|
|
1
|
|
K
|
I,J
|
4
|
|
L
|
F,G
|
5
|
|
M
|
K,L
|
4
|
Du dictionnaire des précédents ci-haut, il en
découle le graphe PERT ci-dessous :
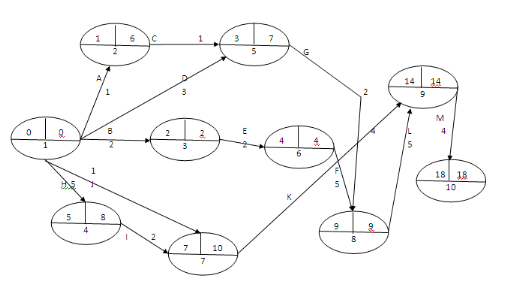
Figure 2.11 : Exemple du graphe Pert
| 


