2.4.1.2 Objectif de la
méthode
La méthode PERT permet de réduire la
durée totale d'un projet par une analyse détaillée des
Tâches ou activités élémentaires et de leur
enchainement. On étudie les délais sans prendre en compte les
charges.
En outre, elle permet :
v La prise en compte des différentes tâches
à réaliser et des antériorités à
respecter entre ces tâches.
v La détermination de la durée globale du projet
et des tâches qui la conditionnent.
v La détermination des tâches pour lesquelles du
temps est disponible (notion de marge).
v La détermination des dates "au plus
tôt" et "au plus tard" pour lancer chaque
tâche.
v La gestion des moyens logistiques (matériel) et
humains (effectif) intervenant sur le projet.
2.4.1.3 Notions de base
La méthode s'appuie en grande partie sur une
représentation graphique qui permet de bâtir un réseau
PERT .Ce réseau PERT étant constitué par des Tâches
et des étapes
Étape : commencement ou fin d'une
Tâche. Une étape n'a pas de durée. On symbolise une
étape (ou noeud) sur le réseau par un cercle.
Figure 2.2 : Représentation d'une
étape avec la méthode PERT
Remarques
- La longueur des arcs n'est pas proportionnelle au temps
d'exécution.
- Pour alléger la représentation, on ne note pas
le nom complet de la Tâche, mais une lettre ou code le
représentant.
2.4.1.4
Représentation graphique des étapes et des Tâches dans un
réseau

Figure 2.3 : Représentation des étapes
et des Tâches avec la méthode PERT
B ne peut commencer que si A est terminée (A
précède B, ou A est antériorité de B) ,C ne peut
commencer que si A et B sont terminées ( A et B précédent
C, ou A et B sont antériorité de C, ou A et B enclenchent C).
En ce qui concerne les Tâches simultanées, nous
dirons qu'elles peuvent commencer en même temps en partant d'une
même étape. D ne peut commencer que si B est terminée.
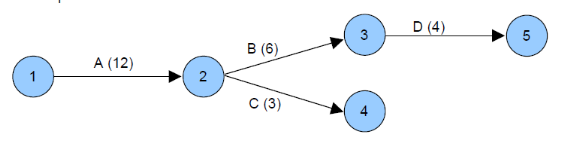
Figure 2.4 : Représentation des tâches
simultanées
Si l'on souhaite que D ne commence que si B et C sont
terminés, On peut améliorer la représentation
précédente pour obtenir:
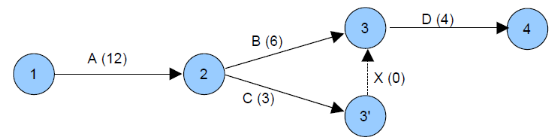
Figure 2.5 : Représentation d'une
tâche virtuelle
Nous noterons en passant que x (0) est une Tâche dite
Tâche fictive qui Sert a représenté ce type de contraintes
de liaison (contraintes d'antériorité). Il s'agit d'une
Tâche dont la durée et le cout sont nuls. On la représente
en pointilles.
Tâches convergentes
Plusieurs Tâches peuvent se terminer sur une même
étape.
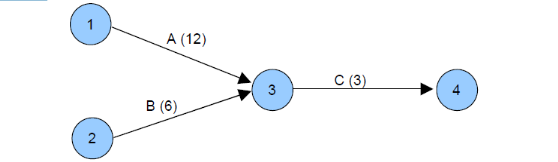
Figure 2.6 : Tâches convergentes
Dans ce cas présent, la Tâche A (12) a une
durée de 12 unîtes de temps, B(6) a une durée de 6
unîtes de temps. On ne constate que la Tâche A dure plus longtemps
que B. A est dite pénalisante
| 


