2.4.2 La Méthode de
Potentiel Métra (M.P.M)
La solution au Problème Central d'Ordonnancement est
donnée par le graphe potentiel (MPM) pondéré et aussi un
réseau de transport quasi-fortement connexe, un cas particulier du
réseau de transport.
2.4.2.1 Eléments du
graphe MPM
Le graphe MPM est constitué des éléments
suivants :
ü Chaque tâche représente un sommet (ou
noeud) ;
ü Chaque arc représente une contrainte de
succession (ou d'antériorité),
ü La pondération (ou potentiel) d'un arc donne le
temps qui doit s'écouler au minimum entre le début de la
tâche origine de l'arc et le début de la tâche
extrémité de l'arc.
2.4.2.2 Principe de la
méthode
A l'identique de la méthode PERT cette méthode
permet de réduire la durée totale d'un projet. On étudie
les délais sans prendre en compte les charges et les moyens
disponibles.
Notions de base
La méthode est une représentation graphique qui
permet de bâtir un réseau.
Ce réseau est constitué par des Tâches (ou
étapes).

Figure 2.12 : Représentation d'une
tâche avec la méthode de potentiel métra
Liaison orientées Elles
représentent les contraintes d'antériorités des
Tâches.
2.4.2.3 Normalisation du
graphe
Le graphe doit comporter un seul début et une seule
fin. Il n'y a pas d'autres
Règles. C'est ce type de graphe qui est le plus souvent
utilisé par les logiciels de planification(comme Microsoft
Project).
2.4.2.4 Méthodologie
de construction d'un graphe potentiel (MPM)
Il sera nécessaire de :
o Etablir la liste des Tâches (faire le partitionnement
des Tâches en fonction des ressources).
o Déterminer des antériorités :
Tâches immédiatement antérieures, et Tâches
antérieures.
o Déterminer les niveaux d'exécution ou rang des
tâches(Très bien détaillé au point 4.2.2.5 sur la
notion des niveaux).
o Construire le réseau MPM.
o Calculer la durée du projet, les dates début
et de fin des Tâches. Déterminer le chemin critique
2.4.2.5 Notion des
Niveaux
Considérons le tableau suivant (dictionnaire de
précédent) :
|
Tâches
|
Antériorités
|
Durées
|
|
A
|
|
1
|
|
B
|
|
2
|
|
C
|
A
|
1
|
|
D
|
|
3
|
|
E
|
B
|
2
|
|
F
|
E
|
5
|
|
G
|
C , D
|
2
|
|
H
|
|
5
|
|
I
|
H
|
2
|
|
J
|
|
1
|
|
K
|
I, J
|
4
|
|
L
|
F, G
|
5
|
|
M
|
K, L
|
4
|
En outre, nous noterons par :
v P(x) :l'ensemble des tâches qui
précède immédiatement les tâches qui sont dans x,si
nous nous referons à notre dictionnaire des précédents(x)
représente la colonne « Antériorités
» et x représente la colonne
« Tâches »
 v v  (x) représentel'ensemble des successeurs de x. (x) représentel'ensemble des successeurs de x.
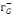 v v 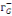 (x) représente l'ensemble des prédécesseurs de
x. (x) représente l'ensemble des prédécesseurs de
x.
Dans la construction du graphe potentiel il est
nécessaire d'ordonner les différentes tâches en niveau.
L'algorithme suivant permet de repartir toutes les
tâches en niveau :
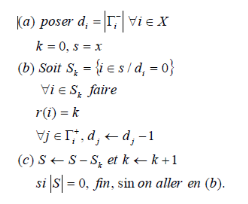
Apres l'application de l'algorithme de niveau, les
tâches du dictionnaire des précédents sont reparties en
ceux-ci :
Niveau 0 : {A, B, D, H, J}
Niveau 1 : {C, E, I}
Niveau 2 : {F, G, K}
Niveau 3 : {L}
Niveau 4 : {M}
| 


