Memoire Online - à‰conométrie financière. Une comparaison entre les données boursières et le chiffre d'affaires Paris.

Cette section présente la partie empirique de nos travaux : la modélisation. Pour cette partie on va seulement suivre les étapes décrites précédemment dans la méthodologie. Les corrélogrammes des variables, pour des raisons explicités dans la méthodologie, ne seront pas être ici discutés.

Afin de stationnariser les séries temporelles en variance, on va plutôt travailler avec des séries en logarithme, d'après Mignon (2008), on peut constater que la transformation d'une série en logarithme diminue le phénomène de l'hetétéroscédasticité. Hendry et Juselius (2000) constatent que si un ensemble de séries est cointégré en niveau, il sera également cointégré en niveau logarithmique.

Premièrement, cinq groupes d'études ont été créé dans le software gretl, un pour chaque entreprise, en ajoutant ses variables financières et comptables. Ensuite, on teste la stationnarité avec le test de Dickey-Fuller augmenté (ADF). Pour le log du chiffre d'affaire de l'entreprise TOTAL SA, si on regarde le graphique de la série temporelle (les résultats sont en puissance de dix écrites avec la notation computationnelle e):

On peut apercevoir que la série n'a pas de tendance stationnaire ni de variance constante, ce qui ressemble à un processus de marche aléatoire. D'après les annexes 6, 7 et 9, on peut remarquer que les autres entreprises ont un comportement similaire à ce qui concerne ces graphiques, à l'exception du graphique de l'entreprise LVMH (annexe 8), d'où on peut constater qui le phénomène de la saisonnalité est très évident (des sommets toujours dans le quatrième trimestre).

Pour être sûr à propos de la stationnarité de la série on va passer le test ADF à partir du software gretl (les valeurs p. critiques sont liées aux valeurs critiques de student). On va comparer les statistiques t avec les valeurs critiques du test ADF, qui sont présentes dans les tableaux 1 et 2, afin de savoir si l'hypothèse nulle est vraie. En regardant le test en trois étapes pour l'entreprise TOTAL SA, la première étape avec le modèle (3) :

Tableau 4: Modèle (3) du test ADF pour le log du CA de l'entreprise TOTAL SA

	^coefficient		^{t de Student}

^const	^5,87805	^2,47770	^2,372	^0,0260
^l_CA_1	^-0,337847	^0,142570	^-2,370	^0,3956
^d_l_CA_1	^0,483413	^0,176323	^2,742	^0,0114
^d_l_CA_2	^-0,0474088	^0,197423	^-0,2401	^0,8123
^time	^0,00322662	^{erreur std.} ^0,00211218	^1,528	^0,1397

Comme la tendance temporelle (time) n'a pas été significative (d'après la valeur critique du tableau 2, de 2.79 à 5% ou de 2.38% à 10%). Si on regarde les statistiques t des annexes 10, 13, 16 et 19, on peut constater que la tendance temporelle n'est pas significative pour les autres entreprises non plus. On passe à l'étape suivante, pour le deuxième modèle :

Tableau 5: Modèle (2) du test ADF pour le log du CA de l'entreprise TOTAL SA

	^coefficient		^{t de Student}

^const	^3,50014	^{erreur std.} ^1,97843	^1,769	^{p. critique} ^0,0891
^l_CA_1	^-0,199027	^0,112747	^-1,765	^0,3983
^d_l_CA_1	^0,457754	^0,180142	^2,541	^0,0176
^d_l_CA_2	^-0,144040	^0,191938	^-0,7505	^0,4600

On observe que la constante (const) n'a pas été significative au seuil de 10% (valeur critique de 2.17 pour la constante du modèle (2)). D'après les annexes (11, 14, 17 et 20), on peut apercevoir que les statistiques t pour les constantes des autres entreprises ont une valeur absolue trop faible, et pour cela on peut conclure qu'elles ne sont pas significatives. Donc on passe à la dernière étape du test :

Tableau 6: Modèle (1) du test ADF pour le log du CA de l'entreprise TOTAL SA

	_coefficient		_{t de Student}

_{l_CA_1}	_0,000172064	_0,000841220	_0,2045	_0,7457
_{d_l_CA_1}	_0,281719	_0,179449	_1,570	_0,1277

Comme la valeur t de la variable (l_CA_1) est trop faible et inférieur à la valeur absolue critique au seuil de 10% de significance (valeur critique de -1.61), d'après le tableau 1, on ne rejette pas l'hypothèse nulle de racine unitaire (ou non stationnarité). D'après les

annexes 12, 15, 18 et 21, on n'a pas rejeté l'hypothèse nulle pour les autres entreprises non plus, ce qui nous oblige à différencier les séries à fin de trouver des séries stationnaires.

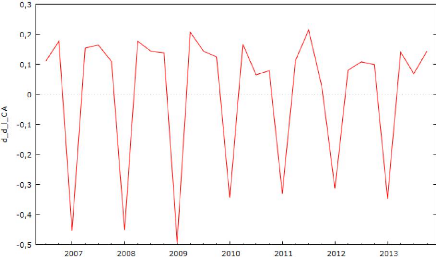
On peut regarder le graphique de la série différencié : Graphique 5 : Log du CA différencié de l'entreprise TOTAL SA

Maintenant, on peut apercevoir que le graphique passe souvent sur la valeur nulle et que sa variance est constante presque tous les temps (à l'exception des périodes de crise). Cela suit les caractéristiques d'une série stationnaire. Si on regarde les annexes 22 et 23, on peut vérifier que les entreprises BNP Paribas et L'Oréal ont un comportement similaire à celui de TOTAL SA. Par contre, d'après l'annexe 25, on constate que le graphique pour l'entreprise Sanofi a une variance très expressive et que ne semble pas constante ce qui semble à une série non stationnaire. Comme le test ne prend pas en compte des caractéristiques d'une série avec saisonnalité, la série différenciée du log du CA de LVMH ne va pas être stationnaire, d'après son graphique (annexe 24), on peut apercevoir que la série différencié a encore un comportement de saisonnalité, qui ne correspond pas à une série stationnaire.

On recommence le test ADF pour le log du CA différencié de l'entreprise TOTAL SA. Pour le troisième modèle:

Tableau 7: Modèle (3) du test ADF pour le log du CA différencié de TOTAL SA

	^coefficient		^{t de Student}

^const	^0,00716634	^0,0351270	^0,2040	^0,8400
^d_l_CA_1	^-0,891631	^0,222727	^-4,003	^0,0086
^d_d_l_CA_1	^0,284764	^0,185167	^1,538	^0,1366
^time	^3,62948e-05	^{erreur std.} ^0,00177139	^0,02049	^0,9838

La tendance temporelle (time) n'est pas significative au seuil de 10% si on compare avec la valeur critique présente au tableau 2. D'après les annexes 26, 29, 32 et 35, on peut constater que la tendance temporelle n'est pas significative pour les autres entreprises non plus. Donc il faut qu'on passe à la prochaine étape. Pour le modèle (2) :

Tableau 8: Modèle (2) du test ADF pour le log du CA différencié de TOTAL SA

	^coefficient		^{t de Student}
		^{erreur std.}		^{p. critique}
^const	^0,00781853	^0,0145678	^0,5367	^0,5960
^d_l_CA_1	^-0,891397	^0,218117	^-4,087	^0,0010
^d_d_l_CA_1	^0,284747	^0,181571	^1,568	^0,1289

Comme la statistique t de la constante est inférieur à la valeur critique au seuil de 10% (valeur critique de 2.17), on trouve qu'elle n'est pas significative, si on regarde les annexes 27, 33 et 36, on peut apercevoir que les résultats sont similaires pour les entreprises BNP Paribas, LVMH et Sanofi. Par contre, d'après l'annexe 30, on observe que la constate à été significative au seuil de 10% (d'après le tableau 2) et on rejette l'hypothèse nulle au seuil de 1% (valeur critique de -3.51), d'après le tableau 1, avec cela on peut arrêter le test de stationnarité pour l'entreprise L'Oréal, parce que son chiffre d'affaire est devenu stationnaire après une différentiation. Par contre, il faut qu'on continue le test ADF pour les autres quatre entreprises. Pour la dernière étape du test :

Tableau 9: Modèle (1) du test ADF pour le log du CA différencié de TOTAL SA

	_coefficient		_{t de Student}
					***
_{d_l_CA_1}	_-0,881115	_0,214390	_-4,110	_4,11e-05
_{d_d_l_CA_1}	_0,277580	_0,178675	_1,554	_0,1319

On peut apercevoir que la statistique t de la variable en question est inférieur à la valeur critique de 1% (-2.60), ce qui nous permet de rejeter l'hypothèse nulle. Après cela, on peut constater que la série différencié est stationnaire. On peut apercevoir, en regardant l'annexe 28, que le log du CA de BNP Paribas est aussi stationnaire quand on prend sa différence première. En contrepartie, si on analyse les annexes 34 et 37, on peut apercevoir que le log du CA différencié des entreprises LVMH, à cause de sa saisonnalité, et Sanofi, à cause de sa variance, n'est pas stationnaire, donc on a besoin de les différencier une autre fois afin de les rendre stationnaires.

On peut apercevoir que le phénomène de la saisonnalité est moins évident maintenant pour le CA de l'entreprise LVMH. Dans les deux graphiques la variance n'est pas

Si on différencie une autre fois le CA pour les entreprises LVMH et Sanofi, on peut observer le nouveau graphique pour l'entreprise LVMH :

assez significative et plus ou moins constante, ce qui est une caractéristique des séries stationnaires.

Tableau 10: Modèle (3) du test ADF pour le log du CA différencié deux fois de LVMH

	^coefficient		^{t de Student}

^const	^-0,0533037	^0,0945157	^-0,5640	^0,5780
^d_d_l_CA_1	^-2,00873	^0,283099	^-7,095	^1,31e-09
^d_d_d_l_CA_1	^0,499192	^{erreur std.} ^0,173176	^2,883	^0,0082
^time	^0,00274186	^0,00468233	^0,5856	^0,5636

Tableau 11: Modèle (3) du test ADF pour le log du CA différencié deux fois de Sanofi

	^coefficient		^{t de Student}

^const	^0,0276510	^0,0571589	^0,4838	^0,6329
^{d_d_l_COURS_1}	^-2,28104	^{erreur std.} ^0,345310	^-6,606	^3,18e-08
^{d_d_d_l_COURS_1}	^0,396165	^0,193878	^2,043	^0,0521
^time	^-0,00138574	^0,00283375	^-0,4890	^0,6293

En comparant les statistiques t des tendances temporelles avec les valeurs critiques présentes dans le tableau 2, on peut apercevoir qu'au seuil de 10%, aucune des tendances n'est significative. À cause de cela, on passe à l'étape suivante, pour l'entreprise LVMH :

Tableau 12: Modèle (2) du test ADF pour le log du CA différencié deux fois de LVMH

			^{t de Student}
^coefficient		^{erreur std.}		^{p. critique}
^const	^-0,00257749	^0,0373034	^-0,06910	^0,9455
^d_d_l_CA_1	^-2,01090	^0,279330	^-7,199	^9,49e-011
^d_d_d_l_CA_1	^0,501999	^0,170820	^2,939	^0,0070	***

Tableau 13: Modèle (2) du test ADF pour le log du CA différencié deux fois de Sanofi

	^coefficient	^{erreur std.}	^{t de Student}	^{p. critique}

^const	^0,00201869	^0,0224465	^0,08993	^0,9291
^{d_d_l_COURS_1}	^-2,26587	^0,338638	^-6,691	^2,19e-09	***
^d_^d_^d_^l_^COURS_¹	^0,387136	^0,190037	^2,037	^0,0524	*

On peut apercevoir que les valeurs des statistiques t des constantes pour les deux entreprises ne sont pas assez fortes, par conséquent les constantes ne sont pas significatives au seuil de 10%. Donc on passe à la dernière étape du test, pour l'entreprise LVMH :

Tableau 14: Modèle (1) du test ADF pour le log du CA différencié deux fois de LVMH



_{d_d_l_CA_1}	_-2,01085	_0,273931	_-7,341	_2,43e-012
_{d_d_d_l_CA_1}	_0,502002	_0,167519	_2,997	_0,0059

Tableau 15: Modèle (1) du test ADF pour le log du CA différencié deux fois de Sanofi

	_coefficient		_{t de Student}

_{d_d_l_COURS_1}	_-2,26565	_0,332108	_-6,822	_4,91e-011
_{d_d_d_l_COURS_1}	_0,387244	_0,186373	_2,078	_0,0477

On peut comparer les valeurs des statistiques t avec les valeurs critiques de racine unitaire (d'après le tableau 1), ce qui nous amène à conclure qu'elles sont significatives au seuil de 1% (valeur critique de -2.60). Avec cela, on déduit que les séries deviennent stationnaires après deux différentiations et on peut terminer les tests ADF pour les chiffres d'affaires.

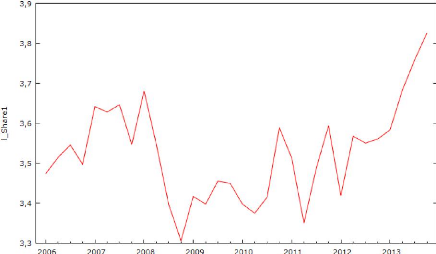
Maintenant, on passe à tester la stationnarité pour la variable dépendante du travail, le cours boursier (COURS). On va travailler avec les logarithmes des cours boursiers pour le même motif explicité au début de la modélisation. Si on regarde le graphique du Log des cours boursiers de l'entreprise TOTAL SA :

On peut observer que la série temporelle a un comportement similaire à une série de marche aléatoire, ce qui semble à une série non stationnaire. D'après les annexes 43, 44, 45 et 46, on constate un mouvement aléatoire dans toutes les graphiques. Afin de savoir à coup sûr, on va tester la stationnarité avec le test ADF. La première étape pour l'entreprise TOTAL SA :

Tableau 16: Modèle (3) du test ADF pour le log des cours boursiers de TOTAL SA

	^coefficient		^{t de Student}

^const	^0,280682	^0,913986	^0,3071	^0,7617
^l_Share1_1	^-0,0928986	^0,259057	^-0,3586	^0,9890
^d_l_Share1_1	^-0,277037	^0,306231	^-0,9047	^0,3754
^d_l_Share1_2	^-0,283570	^0,268913	^-1,055	^0,3031
^d_l_Share1_3	^-0,0704265	^0,237068	^-0,2971	^0,7692
^time	^0,00333827	^{erreur std.} ^0,00249514	^1,338	^0,1946

Comme la statiques t de la tendance temporelle est trop faible, on conclue, en comparant avec le tableau 2, qu'elle n'est pas significative. Si on regarde les annexes 47, 50 et 53, on peut apercevoir que la tendance temporelle n'est pas significative pour les entreprises BNP Paribas, L'Oréal et LVMH non plus. Par contre, d'après l'annexe 56, on conclue au seuil de 5% (valeur critique de 2.79, d'après le tableau 2), que la tendance est significative pour l'entreprise Sanofi, donc on a besoin de tester la racine unitaire, comme la statistique t de la variable en question est trop faible, on ne peut rejeter l'hypothèse nulle (la série est non stationnaire), donc il faut qu'on la différencie. On passe au modèle (2) du test :

Tableau 17: Modèle (2) du test ADF pour le log des cours boursiers de TOTAL SA

	^coefficient		^{t de Student}

^const	^0,469339	^0,918421	^0,5110	^0,6142
^l_Share1_1	^-0,129399	^{erreur std.} ^0,262003	^-0,4939	^{p. critique} ^0,8901
^d_l_Share1_1	^-0,178522	^0,302308	^-0,5905	^0,5606
^d_l_Share1_2	^-0,204275	^0,266767	^-0,7657	^0,4516
^d_l_Share1_3	^-0,0165149	^0,237596	^-0,06951	^0,9452

Après comparer la statistique t de la constante avec les valeurs critiques (tableau 2), on constate qu'elle n'est pas significative au seuil de 10%. Si on consulte les annexes 48, 51 et 54 on peut remarquer que les résultats sont similaires, les constantes pour les entreprises BNP Paribas, L'Oréal et LVMH n'ont pas été significatives. Il faut qu'on continue le test ADF pour le modèle (1) :

Tableau 18: Modèle (1) du test ADF pour le log des cours boursiers de TOTAL SA



_{l_Share1_1}	_0,00334959	_0,00516501	_0,6485	_0,8563
_{d_l_Share1_1}	_-0,209726	_0,186111	_-1,127	_0,2694

La statistique t est trop faible ce qui nous amène à conclure que la variable n'est pas significative au seuil de 10%, on ne peut pas rejeter l'hypothèse nulle (la série est non-stationnaire), il faut qu'on la différencie pour la rendre stationnaire. D'après les annexes 49, 52 et 55, on peut apercevoir que les séries sont non-stationnaires, parce qu'on n'a pas rejette l'hypothèse d'existence de racine unitaire d'après la comparaison entre les statistiques t et les valeurs critiques du tableau 1.

Comme les cours boursiers en logarithme ne sont pas stationnaires, il faut qu'on différencie les séries afin de les rendre stationnaires. On peut analyser le graphique du log des cours boursiers différenciés de l'entreprise TOTAL SA :

Graphique 9 : Log des cours boursiers différenciés de l'entreprise TOTAL SA

On peut constater que la série a sa moyenne centrée en zéro et que sa variance est relativement constante, ce qui correspond à un comportement d'une série stationnaire. D'après les annexes 57, 58, 59 et 60, on peut observer que les autres entreprises ont un comportement similaire à ceux de TOTAL SA. Maintenant on passe au test ADF pour la série différencie. On commence par le modèle (3) pour l'entreprise TOTAL SA :

Tableau 19: Modèle (3) du test ADF pour le log des cours boursiers différenciés de TOTAL SA

	^coefficient		^{t de Student}

^const	^-0,0434535	^0,0428877	^-1,013	^0,3207
^d_l_Share1_1	^-1,62475	^0,298300	^-5,447	^2,18e-05
^{d_d_l_Share1_1}	^0,304577	^0,189227	^1,610	^0,1200
^time	^0,00322198	^{erreur std.} ^0,00218567	^1,474	^0,1529

On constate que la statistique t pour la tendance temporelle est trop faible, donc elle n'est pas significative quand on compare sa valeur avec les valeurs critiques du tableau 2. D'après les annexes 61, 64, 67 et 70, on peut avoir la même conclusion pour les autres entreprises. On continue le test par la prochaine étape :

Tableau 20: Modèle (2) du test ADF pour le log des cours boursiers différenciés de TOTAL SA

	^coefficient		^{t de Student}

^const	^0,00963056	^0,0196630	^0,4898	^0,6291
^d_l_Share1_1	^-1,25533	^0,601752	^-2,086	^0,2505
^{d_d_l_Share1_1}	^0,00956670	^0,503242	^0,01901	^0,9850
^{d_d_l_Share1_2}	^-0,210895	^{erreur std.} ^0,362796	^-0,5813	^0,5669
^{d_d_l_Share1_3}	^-0,211704	^0,214153	^-0,9886	^0,3336

Si on compare la statistique t de la constance avec les valeurs critiques de Dickey-Fuller, on conclue qu'elle n'est pas significative au seuil de 10% (valeur critique de 2.17, d'après le tableau 2). Pour les autres entreprises, selon les annexes 62, 65, 68 et 71, on trouve que les constantes ne sont pas significatives. À cause de cela, il faut qu'on passe à la dernière étape du modèle :

Tableau 21: Modèle (1) du test ADF pour le log des cours boursiers différenciés de TOTAL SA

	^coefficient		^{t de Student}
		^{erreur std.}		^{p. critique}
^d_l_Share1_1	^-1,21125	^0,585070	^-2,070	^0,0369
^{d_d_l_Share1_1}	^-0,0211718	^0,490994	^-0,04312	^0,9660	**
^{d_d_l_Share1_2}	^-0,229447	^0,354801	^-0,6467	^0,5242
^{d_d_l_Share1_3}	^-0,219534	^0,209997	^-1,045	^0,3067

En comparant la statistique t avec les valeurs critiques de racine unitaire du tableau 1, on conclue qu'elle est significative au seuil de 5% (valeur critique de -1.95), donc on rejette l'hypothèse nulle, la série est maintenant stationnaire et on peut arrêter le test ADF. D'après les annexes 63, 66, 69 et 72, on peut rejeter l'hypothèse de racine unitaire pour les autres entreprises aussi.

Comme on a bien trouvé les séries stationnaires après la différentiation, on peut maintenant commencer les tests de cointégration. On estime les paramètres par MCO en introduisant des variables dummies de correction de saisonnalité, ce qui nous permet de travailler même avec les séries qui n'ont pas de racine unitaire dans les variables indépendantes (LVMH et Sanofi). La modélisation par MCO pour l'entreprise TOTAL SA est comme suit :

Modèle 2: MCO, utilisant les observations 2006:1-2013:4 (T = 32)
Variable dépendante: l_Share1

	Coefficient		Erreur Std		t de Student	p. critique
const	-1,6625		2,7005		-0,6156	0,54330
l_CA	0,295532		0,153838		1,9211	0,06534		*
T1	-0,0220082		0,0603018		-0,3650	0,71798
T2	-0,0397488		0,0601486		-0,6608	0,51431
T3	-0,0167468		0,0601588		-0,2784	0,78284
Moy. var. dép.		3,525173		Éc. type var. dép.			0,120628
Somme carrés résidus		0,390673		Éc. type de régression			0,120289
R2		0,133924		R2 ajusté			0,005616
F(4, 27)		1,043771		p. critique (F)			0,403088
Log de vraisemblance		25,08388		Critère d'Akaike			-40,16776
Critère de Schwarz		-32,83908		Hannan-Quinn			-37,73851
rho		0,583789		Durbin-Watson			0,856695

Les annexes 77, 78, 79 et 80 présentent la même modélisation pour les autres entreprises. D'après ces modèles de MCO, on va prendre les résidus afin de tester la cointégration (ou la relation de long terme) entre les variables dépendantes (les cours boursiers) et indépendantes (les chiffres d'affaires). Le test d'Engle-Granger pour l'entreprise TOTAL SA :

^coefficient		^{erreur std.}	^{t de Student}	^{p. critique}

^{l_resid_sais_1}	^-0,349350	^0,253701	^-1,377	^0,1569
^{d_l_resid_sais_1}	^-0,0500037	^0,247398	^-0,2021	^0,8414
^{d_l_resid_sais_2}	^-0,126447	^0,215999	^-0,5854	^0,5633

On va comparer la statistique t avec les valeurs critiques d'Engle et Yoo (d'après le tableau 3), comme elle n'est pas assez forte on conclue qu'au seuil de 10% (valeur critique de -2.90) elle n'est pas significative. Cela indique que les variables ne sont pas cointégrées entre elles, donc il n'existe pas une relation de long terme. D'après les annexes 73, 74, 75 et 76, on peut constater que les valeurs absolues des statistiques t sont inférieurs à les valeurs critiques absolues au seuil de 10%, donc on a la même conclusion pour les autres entreprises, il n'y a pas de relation de long terme entre les variables.

Comme on n'a pas trouvé une relation de long terme entre les variables, on ne peut pas estimer un modèle à correction d'erreur. Quand même, on peut essayer d'estimer une relation de court terme avec les séries stationnarisées. On va continuer à utiliser des variables dummies afin de résoudre des problèmes éventuels de saisonnalité.

On commence par la modélisation de court terme par MCO pour l'entreprise TOTAL SA. On prendre le log des cours boursiers différenciés une fois comme variable dépendante et le log des chiffres d'affaires différenciés comme variable indépendante en ajoutant les variables dummies de saisonnalité :

Modèle 6: MCO, utilisant les observations 2006:2-2013:4 (T = 31)
Variable dépendante: d_l_Share1

	Coefficient		Erreur Std		t de Student	p. critique
const	0,0130686		0,0184859		0,7069	0,48589
d_l_CA	-0,223961		0,23223		-0,9644	0,34373
T1	0,00326834		0,0530074		0,0617	0,95131
T2	-0,0129109		0,0520758		-0,2479	0,80614
T3	0,0127453		0,0512569		0,2487	0,80558
Moy. var. dép.		0,011357		Éc. type var. dép.			0,097742
Somme carrés résidus		0,272360		Éc. type de régression			0,102349
R2		0,049692		R2 ajusté			-0,096509
F(4, 26)		0,339890		p. critique (F)			0,848525
Log de vraisemblance		29,39946		Critère d'Akaike			-48,79891
Critère de Schwarz		-41,62898		Hannan-Quinn			-46,46169
rho		-0,152319		Durbin-Watson			2,275254

On peut apercevoir, d'après la valeur du R² ajusté, que le pouvoir explicatif du modèle est trop faible, en outre, la variable indépendante n'a pas été significative au seuil de 10% d'après la valeur p. critique, donc la relation statistique n'est pas trop forte. On passe à l'estimation de la relation de court terme pour l'entreprise BNP Paribas :

Modèle 3: MCO, utilisant les observations 2006:2-2013:4 (T = 31)
Variable dépendante: d_l_COURS

	Coefficient		Erreur Std		t de Student	p. critique
const	-0,0131812		0,03198		-0,4122	0,68359
d_l_CA	1,19091		0,250651		4,7513	0,00006		***
T1	-0,178337		0,112236		-1,5889	0,12416
T2	-0,0556102		0,0909686		-0,6113	0,54630
T3	-0,0561573		0,0890435		-0,6307	0,53376
Moy. var. dép.		0,003235		Éc. type var. dép.			0,230508
Somme carrés résidus		0,808473		Éc. type de régression			0,176338
R2		0,492810		R2 ajusté			0,414781
F(4, 26)		6,315705		p. critique (F)			0,001089
Log de vraisemblance		12,53512		Critère d'Akaike			-15,07025
Critère de Schwarz		-7,900310		Hannan-Quinn			-12,73303
rho		-0,122873		Durbin-Watson			2,234871

Pour le cas de BNP Paribas, on vérifie que le pouvoir explicatif du modèle est assez significatif (d'après la valeur du R² ajusté) et que la variable indépendante est significative au seuil de 1%, on peut conclure que la relation statistique de court terme est expressive. Maintenant on va estimer la relation de court terme pour l'entreprise L'Oréal :

Modèle 4: MCO, utilisant les observations 2006:2-2013:4 (T = 31)
Variable dépendante: d_l_Cours

	Coefficient		Erreur Std		t de Student	p. critique
const	0,0257661		0,0181012		1,4234	0,16650
d_l_CA	-0,104435		0,273181		-0,3823	0,70535
T1	0,0935905		0,0515365		1,8160	0,08092		*
T2	0,0243706		0,0529019		0,4607	0,64886
T3	0,0324862		0,0501883		0,6473	0,52312
Moy. var. dép.		0,022678		Éc. type var. dép.			0,098435
Somme carrés résidus		0,253792		Éc. type de régression			0,098799
R2		0,126917		R2 ajusté			-0,007404
F(4, 26)		0,944880		p. critique (F)			0,453896
Log de vraisemblance		30,49395		Critère d'Akaike			-50,98791
Critère de Schwarz		-43,81797		Hannan-Quinn			-48,65069
rho		0,152381		Durbin-Watson			1,615571

Comme le R² ajusté du modèle est trop faible, le pouvoir explicatif du modèle est insignifiant. La variable indépendante n'est pas significative au seuil de 10% d'après la valeur p. critique. On ne peut pas inférer significativement sur ce modèle parce que son pouvoir explicatif est trop faible. On passe à estimer la relation de court terme pour la prochaine

étape, LVMH (comme le log du chiffre d'affaire différencié n'est pas stationnaire, on va travailler avec la série différencié deux fois) :

Modèle 3: MCO, utilisant les observations 2006:3-2013:4 (T = 30)
Variable dépendante: d_l_COURS

	Coefficient		Erreur Std		t de Student	p. critique
const	0,0241802		0,0235336		1,0275	0,31404
d_d_l_CA	-0,726442		0,470918		-1,5426	0,13549
T1	-0,2815		0,246057		-1,1440	0,26344
T2	0,0386927		0,0686993		0,5632	0,57830
T3	-0,00598602		0,0646872		-0,0925	0,92701
Moy. var. dép.		0,022697		Éc. type var. dép.			0,130751
Somme carrés résidus		0,413475		Éc. type de régression			0,128604
R2		0,166009		R2 ajusté			0,032571
F(4, 25)		1,244089		p. critique (F)			0,317963
Log de vraisemblance		21,69717		Critère d'Akaike			-33,39434
Critère de Schwarz		-26,38835		Hannan-Quinn			-31,15306
rho		0,055241		Durbin-Watson			1,887621

Le R² ajusté a une valeur trop faible, donc le pouvoir d'explication du modèle n'est suffisant pour avoir une bonne relation statistique. La valeur p. critique pour la variable indépendante est supérieure à 10%, ainsi on peut conclure qu'elle n'est pas significative. On passe à la dernière estimation d'une relation de court terme, l'estimation pour l'entreprise Sanofi (on va travailler avec le log du chiffre d'affaires différencié deux fois pour la même raison de l'entreprise LVMH) :

Modèle 2: MCO, utilisant les observations 2006:3-2013:4 (T = 30)
Variable dépendante: d_l_COURS

	Coefficient		Erreur Std		t de Student	p. critique
const	0,0136852		0,0125237		1,0927	0,28492
d_d_l_COURS	0,500418		0,0960236		5,2114	0,00002		***
T1	0,0362847		0,0378377		0,9590	0,34676
T2	0,0316733		0,0361709		0,8757	0,38955
T3	-0,00283213		0,0350154		-0,0809	0,93618
Moy. var. dép.		0,012155		Éc. type var. dép.			0,101867
Somme carrés résidus		0,117103		Éc. type de régression			0,068440
R2		0,610866		R2 ajusté			0,548605
F(4, 25)		9,811304		p. critique (F)			0,000065
Log de vraisemblance		40,62039		Critère d'Akaike			-71,24077
Critère de Schwarz		-64,23479		Hannan-Quinn			-68,99950
rho		0,533101		Durbin-Watson			0,923259

On peut constater que le R² ajusté a une valeur considérable, ce qui rend le pouvoir d'explication à un niveau assez significatif. La variable indépendante est significative au seuil de 1% d'après la valeur p. critique, donc on peut apercevoir une relation statistique expressive au court terme.

à‰conométrie financière. Une comparaison entre les données boursières et le chiffre d'affaires Paris.

3. MODÉLISATION