III.1.1.2.5. La Méthode de la régression
linéaire
Selon SANDERS & ALLAND, la technique de
la régression linéaire est une méthode statistique qui
nous montre que l'étape principale d'une analyse de régression
consiste à déduire, en se basant sur les données
échantillonnages, une équation d'estimation qui décrit la
nature fonctionnelle de la relation entre les variables(39). Cette
méthode nous a permis

d'étudier e miner a relation statistique entre les deux
variables de notre étude (les
coû los ansort et la reforme du chiffre d'affaires). La
formule est la suivante:
T=
D'où
n = taille de l'échantillon.
a = y-tx
Où X = la moyenne de la variable x
T = constante
36 GRAWITZ, Madeleine: Méthodes de recherche en
sciences sociales, Dalloz, Paris, 2001, p.40
49
Y = la moyenne de la variable y
Cette mesure est appelée « l'erreur type de
l'estimation et son symbole est Sy.x. Elle est utilisée pour quantifier
le degré de variation ( ou erreur ) possible associée à
une estimation obtenue à partir de la droite de
régression.
La formule de Sy.x est la suivante:
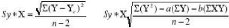
ou
La première formule s'avère très
utile pour expliquer ce qu'est l'erreur type de l'estimation, mais la formule
qui est plus simple à utiliser.
Comme vous pouvez le constater, toutes les valeurs
faisant l'objet de cette formule visent à déterminer
l'équation de régression.
| 


