II.2.2.2 LES DISTANCES ENTRE VARIABLES
Dès lors que l'on se situe dans un disque, ou une
sphère, ou une hypersphère au-delà de trois dimensions,
les proximités sont mesurées par des ANGLES. Voyons ceci. Partons
de la distance euclidienne entre deux variables J et j'.
Équation 9: Distance
euclidienne
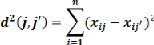
Développons cette identité remarquable.
Équation 10: Equation 9 sous la forme
développée
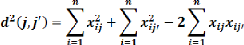
Les deux premiers termes sont égaux à 1 puisque
ce sont des carrés de distances à l'origine. Plus
intéressant est le dernier (enfin quelqu'un qui n'est pas
forcément égal à 1 dans cette histoire...). On retombe
cette fois sur la formule de la covariance entre deux variables centrées
et réduites, c'est-à-dire à un coefficient de
corrélation. Si l'on reprend la formule ci-dessus pour lui appliquer une
corrélation parfaite entre deux variables, on obtient 1 + 1 - (2 ×
1) = 0. Distance nulle. Au pire, le coefficient vaut -1, ce qui donne 1 + 1 + 2
= 4. La distance au carré maximale est de 4, donc la distance maximale
vaut 2. Graphiquement, les deux points représentatifs des variables sont
à l'opposé d'un cercle de rayon 1. Tout ceci est très
logique... Idem si le coefficient est nul. Les points représentant nos
deux variables sont séparés d'un quart de cercle. Les vecteurs
sont orthogonaux. Leur produit scalaire est nul. Car c'est bien là
26
une autre façon d'appréhender les
proximités dans une hypersphère : les produits scalaires. Il est
d'ailleurs assez intuitif que la proximité entre deux vecteurs est
mesurée par l'angle qu'ils forment, donc par le cosinus (pour peu que
ces points soient proches du cercle).
27
| 


