II.2.1.3 ANALYSE DE SENSIBILITE DU MODELE
Dans une analyse de sensibilité locale, les
paramètres sont modifiés un par un de la base d'exécution
par petits incréments (généralement de quelques pour
cent). L'impact du changement des paramètres sur les observations
simulées est évalué. Une mesure typique de la
sensibilité des paramètres est la sensibilité à
l'échelle composite (équation 7) (CSS, Hill et Tiedeman, 2007)
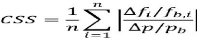
Équation 7: Sensibilité à
l'échelle composite
24
25
Où n est le nombre d'observations simulées, f bi
est la ième observation simulée dans la période de base,
· F je est la modification de l'observation simulée ième
entre le brin perturbé et le brin de base, p b est la valeur du
paramètre dans le cycle de base et
· p b est la variation de
paramètre entre le brin perturbé et la piste de base Les valeurs
CSS sont calculées pour tous les paramètres du modèle
pertinents. CSS donne une idée de l'importance des différents
paramètres en termes d'amélioration ajustement du modèle.
L'analyse de sensibilité doit être effectué avant le
calibrage automatique et les paramètres insensibles doit être
exclu de la liste des paramètres d'étalonnage avant le calibrage
automatique
II.2.2 ANALYSE STATISTIQUE
L'analyse en composantes principales (ACP) est une analyse
factorielle sur variables quantitative. Il s'agit du cercle des
corrélations, qui se met en quatre pour montrer les informations.
Grâce à lui il est commode d'interpréter les composantes
principales. Elle s'illustre comme suite :
Soit une distribution bivariée. Les variables sont
centrées. Le centrage consiste à retirer la moyenne de chaque
valeur prise par la variable brute. Par conséquent, la variable
centrée a pour moyenne 0. Cette translation est très courante en
statistiques. Généralement, les variables sont aussi
réduites. La réduction consiste à diviser la variable
centrée par son écart-type. Ainsi, deux variables centrées
et réduites ont non seulement la même moyenne nulle, mais aussi la
même dispersion égale à 1. On peut choisir de ne pas
réduire les variables et l'on situe alors dans le cadre un peu
particulier d'une ACP non normée (que nous ne verrons pas sur cette
page). Graphiquement, un nuage de points-variables est situé dans un
espace vectoriel à n dimensions, soit autant que
d'unités statistiques (que l'on supposera ici non
pondérées).
II.2.2.1 LA DISTANCE A L'ORIGINE
La métrique utilisée est la distance
euclidienne. Pour un point xi d'une variable donnée, c'est donc
le carré de son écart par rapport à l'ORIGINE (puisqu'en
l'occurrence, on mesure des distances par rapport à une moyenne nulle).
L'ACP sur variables se distinguera donc de l'ACP sur les individus pour
laquelle le nuage de points est centré sur son barycentre. Il suffit
pour s'en convaincre de faire un détour en page effet taille. Cette
fameuse métrique euclidienne est non seulement la plus
célèbre des façons de mesurer une distance mais c'est
aussi celle qui est habituellement utilisée en statistiques. En effet,
on note un air de famille évident avec la formule de la variance
(équation 8):
Équation 8: Variance
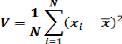
On voit qu'il suffit de multiplier cette formule par N
pour obtenir une distance euclidienne. Comme la variance de chaque
variable est égale à 1, chaque longueur de variable au
carré est égale à 1. L'écart-type étant la
racine carrée de 1, donc 1 également, la norme est aussi
égale à 1. C'est le rayon du cercle dans lequel s'inscrivent les
points-variables.
| 


