II2.2.3 Maillage
Les calculs numériques effectués par la
méthode des éléments finis s'appuient sur un maillage
(discrétisation spatiale) associe à la géométrie du
domaine dans lequel on désire effectuer la simulation. Leur
précision dépend de la taille des éléments (le pas
de discrétisation spatiale). Plus ces derniers sont petits plus les
calculs sont précis et plus la simulation est fiable. En pratique, il
n'est pas possible de raffiner uniformément la taille des
éléments autant que nécessaire, pour des raisons
évidentes de temps et de coûts de calculs. Toutefois, il est
possible de raffiner le maillage dans les zones critiques de la tubulure
simulée.
Dans notre étude, les zones les plus sensibles et qui
demandent par conséquent un raffinage sont la zone de contact
métal de base/métal d'apport et les interfaces entre les passes
dans le cas du soudage multipasses.
? Choix du maillage
Une étape cruciale dans la simulation numérique
de tout problème physique par la méthode des
éléments finis est la génération d'un maillage
associe à la géométrie du domaine considéré.
La construction du maillage est un processus d'autant plus délicat quant
il s'agit de simuler un problème industriel dans lequel les
géométries sont très arbitraires et très souvent
complexes. D'après le principe de la méthode des
éléments finis, la qualité de la solution
47
dépend fortement de celle du maillage. Par
conséquent, dans un problème donné, le maillage construit
par l'une ou l'autre des techniques doit satisfaire un ensemble de contraintes
liées à la qualité requise de la solution, on parle ainsi
d'adaptation de maillage.
Les techniques d'adaptation de maillage ont largement fait
leurs preuves autant pour améliorer la qualité (par exemple en
termes de précision) d'une solution que pour réduire le temps du
calcul. Pourtant il existe encore très peu de logiciels de simulation
intégrant cette capacité [17].
Pour notre cas, le maillage a été
régénéré automatiquement par le logiciel de calcul.
A noter que les zones critiques ont été raffinées
manuellement. Le modèle géométrique est subdivisé
en 2597 éléments avec un nombre total de noeuds, égal
à 8802. La même discrétisation est utilisée pour les
deux types de soudage (mono et multipasses), comme le montre la figure II.5.
Les éléments sont linéaires de types
quadrilatéraux, connus sous le nom du code de calcul " Plane 13 " (voir
la figure II.4).
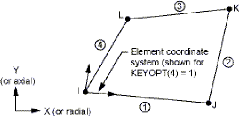
Figure II.4 : Géométrie de
l'élément fini " Plane 13 " [19].
L'élément Plane 13 est un élément
bidimensionnel à quatre noeuds avec trois degrés de
liberté par noeud (déplacements et température). Cet
élément peut être utilisé pour un calcul
couplé thermique-structural en même temps.
La figure II.5 montre la structure simulée
maillée en élément Plane 13 (cas de soudage à 13
passes), le maillage est raffiné au niveau de contact entre le
métal d'apport et le métal de base, et au niveau du contact entre
les différentes passes. Pour le cas de soudage monopasse ou à 3
trois passes, on conserve la densité et la répartition des
éléments tout en assurant un regroupement de tout les surfaces
qui représentent les passes pour construire une seule passe, ou bien les
regrouper trois à trois pour construire le modèle à trois
passes.

Chapitre II Modélisation du procédé de
soudage d'un tube
48
Figure II.5 : Discrétisation de la
tubulure en éléments finis.
| 


