Conclusion
Dans ce chapitre, après avoir donné les
motivations et les objectifs du calcul parallèle, nous avons
présenté un certain nombre de concepts importants pour le calcul
haute performance (HPC) via le parallélisme. En particulier, on a fourni
des concepts généraux et terminologies utilisés dans le
contexte des multiprocesseurs. La populaire classification de Flynn a
été fournie. Nous avons donné les caractéristiques
explicites des architectures SISD, MISD, SPMD, SIMD et MIMD. Cette
classification est aujourd'hui obselète. La plupart des machines
parallèles sont MIMD à savoir l'architecture à
mémoire partagée qui regroupe les calculateurs multiprocesseurs
qui ne permet pas le passage à l'échelle contrairement à
l'architecture à mémoire distribuée qui regroupe les
calculateurs multiordinateurs. Nous avons présenté un cas
particulier des multiordinateurs à savoir l'architecture des grappes de
calcul, plus particulièrement celles hétérogènes.
Ces dernières constituera notre architecture cible dans le cadre de
notre travail. On a vu que deux grands modèles de programmation sont
utilisés sur les architectures distribuées de type grappe de
machines le passage de messages et la mémoire partagée. Dans
notre travail on utilisera le premier modèle et plus
précisément le standard MPI qui est doté de
caractéristiques favorables à notre machine cible. Nous avons
étudier comment analyser les performances d'une application
parallèle avec des postulats de Flynn et Gustafson en utilisant les
paramètres d'accélération et d'efficacité. Une fois
qu'on connaît parfaitement les spécificités de notre
architecture cible tant matérielle que logicielle, il nous revient de
bien représenter notre application parallèle pour pouvoir
l'exécuter sur les ressources de calcul. Dans le chapitre suivant nous
verrons comment représenter une application parallèle de
manière plus formelle en graphe et quels sont les différents
modèles qu'on peut utiliser pour ordonnancer les tâches.
Chapitre II
CONCEPTS D'ORDONNANCEMENT
A
Près que notre application soit conçue et
réalisée en ensemble de tâches, une assignation de ces
tâches aux processeurs de notre architecture doit être
déterminée. Ce problème est appelé problème
d'ordonnancement et est connu comme étant le plus grand défi dans
le domaine du calcul distribué
et parallèle. Le but de l'ordonnancement est de
déterminer une bonne allocation des tâches aux processeurs de
l'architecture. Un algorithme d'ordonnancement prend en compte une
représentation de l'application sous forme de graphe de
précédence, de flots de données ou de tâches et
consiste à répartir ces tâches sur les différents
processeurs du système en fonction d'un critère de performance
donné. Certains modèles d'ordonnancement ont des supports de
communication entre les processeurs de la machine cible tandis que d'autres
négligent l'influence des communications entre les processeurs de la
machine cible. Nous les présenterons et illustrerons après avoir
décrit les différentes représentations d'une application
en tâches par un graphe.
1 Modélisation d'une application
L'algorithme est faite principalement de deux façons,
chacune utilisant un graphe orienté comme structure de base. Nous
pouvons représenter un programme par un graphe de flots de
données (data-flow graph), par un graphe de
précédence(precedence task graph) [5]. En dehors de ces
deux types, nous avons un autre type plus général : le graphe de
tâches(task graph). Dans la suite, nous caractérisons ces
représentations sous la forme d'un graphe orienté sans cycle
(C, V ) où G est l'ensemble des sommets et V est l'ensemble des
arcs. Un graphe de tâches est composé des noeuds
représentant les tâches et les arcs représentant les
dépendances entre les tâches. Nous utilisons le programme
ci-dessous (figure II-1) pour donner un exemple de ces types de graphe.
1.1 Graphe de précédence
Dans la représentation d'un programme par un graphe de
précédence, l'algorithme est divisé en unités de
base dénommées tâches (qui sont des instructions ou groupes
d'instructions). Les tâches sont représentées par des
sommets du graphe. Les dépendances entre les tâches sont
explicitées par des arcs. L'existence d'un arc (u, v) d'une
tâche u à une tâche v dans le graphe
signifie que la tâche v ne peut pas être
exécutée sans les données produites par la tâche
u. Nous associons à chaque arc un poids proportionnel à
la quantité de données à transmettre, et à chaque
sommet un poids correspondant au

Figure II.1 - Exemple de Programme
temps de calcul de la tâche. Dorénavant, nous
ferons référence à cas valeurs comme poids de l'arc ou du
sommet. Lorsque les arcs ne sont pas associés à des poids, c'est
à dire seules les dépendances entre les tâches sont
données, nous avons la représentation par graphe de
dépendance.
Un graphe de précédence est donné en
exemple dans la figure II.2 où les tâches sont
représentées par des cercles et les relations de
précédence par des arcs. Les dépendances étant
introduites pour régler des conflits d'accès à des
données, elles peuvent être interprétées comme des
communications entre les tâches. Dans ce type de graphe, une tâche
est considérée comme prête dès que toutes les
tâches qui la précèdent dans le graphe sont
terminées.
1.2 Graphe de flots de données
Si les dépendances entre tâches sont
considérées comme des communications d'échange de
données, le graphe de flots de données est construit à
partir de l'évolution des données. Les relations de
précédence sont induites par la circulation des données.
Typiquement, les sommets correspondent à l'évaluation d'une
instruction et les précédences aux accès en lecture ou
écriture des opérandes [10]. Un graphe de flots de données
est un graphe biparti, où sont représentées les
tâches et les données. La figure II.3 représente le graphe
de flots de données pour une exécution du programme du calcul de
fibonacci. Connaissant une représentation d'un programme par un graphe
de flots de données, sa transformation en graphe de
précédence est immédiate car le premier fournit plus
d'informations que le dernier. La différence entre les graphes de
précédence et de flots de données se situe au niveau des
synchronisations. Dans le graphe de flot de données, une tâche est
considérée comme prête dès que les données
qu'elle a en entrée sont disponibles. Notons néanmoins qu'un
graphe de flots de données contient les informations d'un graphe de
précédence.
A priori, les tâches peuvent être quelconques et le
graphe de précédence inconnu au moment de

Figure II.2 - Un graphe de
précédence pour le programme. Les tâches sont
représentées par des cercles et les arcs représentent les
précédences.
l'exécution d'un programme. Pour un graphe de
précédence G donné, nous adoptons la terminologie suivante
:
Successeurs : l'ensemble des successeurs d'un
sommet v est constitué de tous les noeuds u tels qu'il
existe un chemin orienté de v à u dans G.
Successeurs directs : l'ensemble des successeurs
directs d'un sommet v est constitué de tous les noeuds u
tels qu'il existe un arc de v à u dans G.
Prédécesseurs : l'ensemble des
prédécesseurs d'un sommet v est constitué de tous les
noeuds u tels qu'il existe un chemin orienté de u
à v dans G.
Prédécesseurs directs : l'ensemble
des prédécesseurs directs d'un sommet v est
constitué de tous les noeuds u tels qu'il existe un arc de
u à v dans G.
Largeur : le cardinal du plus grand ensemble de
sommets du graphe tel qu'il n'existe pas deux sommets appartenant au même
chemin orienté.
Chemin critique: le plus long chemin
orienté du graphe, prenant en compte les temps de calcul.
Granularité : rapport entre le poids des sommets et des
arcs. La granularité p d'un graphe orienté G est le
rapport entre le plus petit poids d'un sommet et le plus grand poids d'un arc
de G. Si p < 1 alors le graphe est dit à grain fin, sinon il
est dit à gros grain. Intuitivement, les tâches d'un graphe
à gros grain calculent plus qu'elles ne communiquent.
Pour illustrer ces terminologies, dans le graphe
orienté G de la figure II.4, nous avons (v8, v9,
v10, v11) pour successeurs du sommet v5. Les
successeurs de v2 sont (v6 , v11). Les
prédécesseurs directs de v9 sont (v5,
v7). La largeur du graphe G est de 4. Si toutes les tâches du
graphe G ont le même poids, le graphe a trois chemins critiques :
(v1, v3, v7, v9), (v1,
v4, v7, v9) et (v1, v5,
v8, v10).

Figure II.3 - Un graphe de flots de
données pour le programme. Les tâches sont
représentées par des cercles. Les données à
transférer dans un rectangle.

Figure II.4 - Graphe de
précédence G
1.3 Graphe de tâches
Dans ce type de graphe (figure II-5), un sommet du graphe
représente un calcul local à un processeur. Ces calculs locaux
sont nommés tâches. Les arcs du graphe
représentent les contraintes de précédence entre calculs.
Par exemple un arc peut modéliser le fait qu'une tâche attend un
résultat produit par une autre tâche.
Le graphe peut être pondéré. La
pondération d'un noeud représente le coût (nombre
d'instructions, temps, etc.) du calcul associé à ce noeud. La
pondération d'un arc représente le volume de données
à transmettre d'un noeud à un de ses successeurs.1
Une tâche est prête si tous ses
prédécesseurs ont déjà été
exécutés et que les données utiles, calculées par
les prédécesseurs de la tâche ont été
acheminées dans la mémoire locale du processeur où vont
avoir lieu les calculs.
Si les données sont déjà présentes
localement, elles n'ont pas besoin d'être communiquées. Le
coût de transfert de données entre deux tâches
exécutées par le même processeur est donc
considéré comme nul.
Si les données ne sont pas présentes localement,
il va falloir les communiquer. Une tâche ne devient prête que
lorsque toutes les données en provenance de tous ses
prédécesseurs sont finalement arrivées. La date à
laquelle elle devient prête dépend donc du nombre de
prédécesseurs, du volume des données à
transférer et du temps que va mettre le réseau pour effectuer
chacun de ces transferts.
Les différences entre les modèles
d'exécution correspondent à des différences dans
l'évaluation du coût de telles communications. Ces
différences ont un impact sur les stratégies d'ordonnancement. Un
exemple de graphe de tâches correspondant au programme du Fibonacci
ci-haut est illustré ci-dessous.

Figure II.5 - Exemple de graphe de
tâche du programme. Les chiffres en bleu représentent les
coûts de chaque tâches. Ceux en noir représentent le volume
des données à transférer d'une tâche à
l'autre par unité de temps.
'Contrairement, au graphe de flots de
données, les données ne seront pas représentées
mais plutôt le volume des données à transmettre. Egalement,
en plus des tâches représentées dans le graphe de
précédence, leur coût de calcul seront
représentés.
L'ordonnancement des calculs et le placement des
données sont deux facteurs importants pour concevoir une application
parallèle efficace; nous présentons par la suite les
modèles typiques d'ordonnancement que l'on rencontre dans la
littérature .
2 Les Modèles classiques
d'ordonnancement
Le comportement réel d'une application est relativement
facile à prévoir en séquentiel. On peut aisément
approcher le temps d'exécution d'un programme, en étudiant par
exemple sa complexité. En parallèle, d'infimes variations dans
l'environnement d'exécution, que ce soit sur un noeud de calcul ou sur
la rapidité du réseau, peuvent changer complètement le
temps d'exécution d'un algorithme non déterministe sensible aux
synchronisations. Quelques outils de réexécution
déterministes. existent et peuvent faciliter le débogage des
applications. Le comportement réel d'une application est donc
très souvent difficile à prévoir, et plus encore à
optimiser. Dans une exécution séquentielle, les portions de code
où le programme passe le plus de temps, sont facilement identifiables.
En parallèle, l'optimisation du code n'est pas suffisante, il faut aussi
que l'ordre des opérations et leurs lieux d'exécution soient
judicieusement choisis. Dans le cas contraire, même si chaque
opération se déroule rapidement, les processeurs de la machine
peuvent rester inactifs en attendant des données calculées sur
d'autres processeurs. Le problème de ce choix est nommé autrement
problème d'ordonnancement. Le temps d'exécution va donc
dépendre de toutes les charges de calculs de tous les processeurs et de
la charge du réseau. En pratique, pour pouvoir concevoir et
évaluer des algorithmes, les machines parallèles sont
modélisées plus ou moins finement. Les différences entre
les modèles concernent principalement la modélisation des
communications. Pour qu'un ordonnancement soit valide, Une
tâche ne débutera son exécution que lorsque ses
prédécesseurs directs ont terminé leurs exécutions
et lorsque les données nécessaires pour leurs exécutions
sont présentes sur les machines sur lesquelles elles
s'exécuteront respectivement.
En d'autres termes, il faut qu'il respecte les contraintes de
précédence et du volume des données à communiquer
entre les tâches. Ces contraintes dépendent du modèle de
coût des communications.
2.1 Modèles à coût de communications
nul
Beaucoup de travaux ont été menés en
négligeant l'influence des communications. Cette hypothèse est
plus ou moins réaliste. Elle est justifiée pour les applications
dont les coûts de calcul sont très grands devant les coûts
de communication et pour des exécutions se déroulant sur des
machines parallèles à mémoire partagée.
Ordonnancer un graphe sans tenir compte des coûts de
communication est relativement facile. De très bonnes garanties de
performance peuvent être obtenues avec des heuristiques simples, par
exemple, en commençant à exécuter une des tâches
prêtes sur le premier processeur qui devient disponible. Quel que soit
l'ordre dans lequel les tâches sont placées, l'exécution
dure moins de 2 fois plus longtemps que le meilleur ordonnancement. Pour
être précis, la garantie est au pire de 2- m,
où m est le nombre de processeurs de la machine.
En fonction du graphe de précédences, de bien
meilleures approximations peuvent être trouvées. Par exemple, si
toutes les tâches sont indépendantes, en plaçant la plus
grosse tâche d'abord, on obtient un rapport de performance avec le
meilleur ordonnancement de 4/3. L'exemple des tâches indépendantes
est en fait pleinement approximable. Pour tout €, un
ordonnancement s'exécutant en moins de 1+ fois le temps du meilleur
ordonnancement peut être construit en temps polynômial (
polynôme en n, le nombre de tâches, et ~ ). En
pratique, ce modèle est réaliste dans deux cas :
- la mémoire de la machine parallèle est
physiquement partagée. Il n'y a pas de communications car les
données sont toujours «locales»;
- le coût de calcul de chaque tâche est très
grand devant le coût d'une communication. Les com-
munications n'influencent pas réellement le temps
d'exécution si l'algorithme est déterministe.
Un premier modèle plus général consiste
à prendre comme modèle du temps d'acheminement des données
de la mémoire d'un processeur à un autre, une fonction de la
taille des données.
2.2 Modèle délai
La première extension possible est de considérer
un délai d constant, lors de la transmission d'un message dans
le réseau entre deux tâches situées sur des processeurs
différents. Ce délai est une fonction de la taille des
données à acheminer. Les processeurs peuvent calculer librement
sans être «gênés» par les communications. Il n'y a
pas, dans ce modèle, de contention (embouteillage) sur le
réseau.
L'ordonnancement dans ce modèle est
généralement plus difficile que l'ordonnancement avec coût
de communication nul. La difficulté d'ordonnancer un graphe de
tâches dans ce modèle dépend du rapport entre le plus petit
coût de calcul d'une tâche et le plus grand coût de
communications entre deux tâches.
1. Dans les problèmes dits à petit temps de
communications, le coût de communication est plus petit que le coût
de calcul. Ce sont des problèmes relativement simples car ils sont
proches des algorithmes sans communication..
2. Dans les problèmes dits à grand temps de
communication, le coût de communication est plus grand que le coût
de calcul. Trouver une solution proche de la solution optimale devient plus
difficile dans le cas général. Il est possible de limiter le
nombre de communications en dupliquant des tâches.
Lorsqu'une application parallèle est
considérée à son grain le plus fin, le coût des
communications est souvent bien supérieur à celui des quelques
calculs locaux. En pratique, des algorithmes de regroupement linéaire
sont utilisés pour ordonnancer ces graphes. Ils consistent à
diviser le graphe en chaînes critiques. Une chaîne critique est un
chemin dans le graphe avec des communications de coût important. Une
chaîne est exécutée par le même processeur. Le
problème revient alors à distribuer ces chaînes sur les
processeurs en essayant de minimiser le coût des communications entre
chaînes. Ceci peut être fait par un algorithme de partitionnement
de graphe non-orienté. Malheureusement, ces algorithmes ont des
garanties de performance qui dépendent du coût de la plus grande
chaîne de communication.
Approximations faites dans le modèle
délai
En fait, le modèle délai néglige deux
aspects importants de la modélisation des communications d'une
application parallèle :
- le surcoût d'exécution dû à la
gestion des communications : Pile de protocole à l'envoi et à la
réception, interruptions, etc. A cela, on peut encore ajouter les
éventuelles copies de mémoires lors des communications. Dans le
modèle délai, un grand nombre de communications peut être
fait sans surcoût, tant que ces dernières sont recouvertes par du
calcul.
- la contention due aux goulots d'étranglements du
réseau. Dans les algorithmes par phases, tous les processeurs ont
tendance à envoyer et recevoir leurs messages en même temps.
Suivant l'architecture et la performance du réseau, cela peut
entraîner un ralentissement important dans la vitesse d'acheminement d'un
message.
Ces deux aspects sont partiellement pris en compte par deux
autres modèles, logP et BSP.
2.3 Les modèles LogP et
BSP
Ces deux modèles sont un raffinement du modèle
délai pour être plus proche du comportement matériel :
LogP modélise plus finement le coût d'une communication
tandis que BSP est en fait un modèle de machine et
d'exécution.
LogP
Le modèle LogP est une extension du
modèle délai plus proche du véritable comportement d'une
machine parallèle. C'est un modèle multiprocesseurs à
mémoire distribuée dans lequel les processeurs font des
communications point à point. Le modèle spécifie les
caractéristiques de performance du réseau d'interconnexion mais
ne décrit pas la structure du réseau. Les paramètres
principaux du modèle sont :
L(Latency) : le temps de transmission d'un
court message d'un processeur source à l'autre.
o(Overhead) : le surcoût en temps
nécessaire au processeur pour recevoir (or) et
transmettre un message (os), durant lequel le processeur ne
peut effectuer d'autres opérations.
g(Gap) : L'intervalle de temps minimum entre
deux transmissions consécutives ou deux réceptions
consécutives sur un processeur. 1/g est le débit de communication
par processeur.
P(Processor) : le nombre de processeurs (les
éléments processeur et mémoire ) dans le réseau.
Le modèle LogGP est une extension du
modèle LogP et il ajoute un paramètre pour prendre en
compte le débit pour les longs messages. Ce paramètre est :
C : Gap par octets pour les longs messages.
On suppose que le réseau a une capacité finie,
telle que au plus [L/g messages peuvent être en transit d'un processeur
à un autre chaque fois. Si un processeur essaie de transmettre un
message qui dépassera cette limite, jusqu'à ce que le message
soit envoyé en respectant la capacité limite.
La figure II.6 schématise ce modèle et la figure
II.7 donne un exemple illustratif.
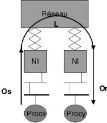
Figure II.6 - Le modèle LogP
BSP
Le modèle BSP (Bulk-synchronous Parallel) sert
à rendre les algorithmes parallèles et leur analyse assez
détaillé pour qu'on puisse en tirer des prévisions assez
réalistes sur le temps de calcul. Son principe de base est de concevoir
toute architecture parallèle comme réseau d'ordinateurs
séquentiels complets et de la quantifier par un petit nombre de
paramètres numériques. Dans le modèle BSP, une machine
parallèle à mémoire distribuée est décrite
en termes de trois éléments :
- Les modules processeur/mémoire,

Figure II.7 - A gauche nous avons une
représentation de l'ensemble des processeurs P=8, L=6,
g=4, o=2 et à droite l'activité de chaque
processeur dans le temps. Le nombre montré pour chaque noeud est le
temps auquel chaque processeur a reçu les données et peut
commencer à envoyer.
- Le réseau d'interconnexion,
- Un synchroniseur qui effectue une barrière de
synchronisation.
Un calcul est une séquence de super-étapes.
Pendant une super-étape, chaque processeur effectue un calcul local,
reçoit et envoie des messages et est sujet aux contraintes suivantes le
calcul local ne doit dépendre que des données présentes
dans la mémoire locale du processeur au début de la
superétape et un processeur doit envoyer au plus h et recevoir
au plus h messages dans une super-étapes. Une telle
communication est appelée une h-relation.
Les modèles d'exécution servent de base à
la programmation d'une machine parallèle. Il donne la sémantique
d'exécution. Un des principaux buts des modèles
d'exécution est de servir à la prédiction du temps
d'exécution d'un programme parallèle. Nous nous
intéresserons aux machines MIMD. Les processeurs sont identiques c'est
à dire qu'ils ont la même vitesse de traitement. Les
modèles de machines que nous avons décrit au chapitre 1 servent
à classer les machines existantes mais ils ne sont pas suffisants lors
du développement d'une application. Si nous voulons connaître le
traitement des conflits lors de l'accès à une donnée
partagée, ou les formes de communication entre les processeurs, nous
avons besoin des modèles d'exécution.
3 Modèles d'exécution et
ordonnancement
Il est clair que le modèle d'exécution doit
être adapté au modèle de machine. Un modèle
d'exécution qui ne prend pas en compte le temps d'accès à
une donnée distante s'avère peu pratique pour une machine MIMD de
type NUMA. Nous allons diviser la présentation des modèles selon
leur origine. Nous présenterons des modèles théoriques,
c'est-à-dire ceux qui n'ont pas été inspirés de
machines existantes d'une part et des modèles basés sur les
caractéristiques de machines réelles d'autre part.
3.1 Le modèle PRAM
Le modèle PRAM (Parallel Random Access
Machine) est un modèle théorique utilisé en calcul
parallèle et qui a servi de raffinement pour obtenir d'autres
modèles. Il est le premier modèle à avoir
été proposé pour l'informatique parallèle
[? ]. Encore aujourd'hui il sert de référence.
Il est très populaire pour l'évaluation et la comparaison
d'algorithmes parallèles [17]. Ce modèle comprend une
unité de contrôle, des processeurs identiques fonctionnent en
cadence par cycle d'une instruction, et qui ont accès à une
mémoire globale commune. En dehors de la mémoire globale, chaque
processeur a
sa mémoire locale. Le nombre de processeurs ainsi que
la taille de la mémoire sont illimités. Ce modèle se
révèle irréaliste en pratique, car le coût de
maintien d'une mémoire globale dépend du nombre de processeurs.
Dans le but de définir les règles d'accès à la
mémoire dans le modèle PRAM, plusieurs versions ont
été proposées. Les types sont :
- le EREW (Exclusive Read Exclusive Write), où chaque
cellule est accédée par au plus un processeur à chaque
cycle,
- le CREW (Concurrent Read Exclusive Write),
- le CRCW (Concurrent Read Concurrent Write), où
l'accès aux cellules peut se faire par plusieurs processeurs pour la
lecture, et pour la lecture et écriture, respectivement.
Dans le dernier cas, des règles de résolution de
conflits sont définies. Les plus courantes, en ordre croissant de
complexité sont : arbitraire, prioritaire et
combinaison de valeurs (par un maximum, une somme, etc). Dans les
modèles du type PRAM les problèmes de communication sont
masqués. La communication est incluse implicitement dans le
modèle. Pourtant en pratique c'est un point important dont il faut tenir
en compte. La figure II.8 illustre les composants du modèle PRAM.

Figure II.8 - Le modèle PRAM pour le
calcul parallèle
3.2 Les modèles avec délai de
communications
Dans les modèles avec délai de communication, il
existe un support pour la communication entre les processeurs. Ce support
consiste en l'envoi et la réception de messages. Dorénavant nous
dénotons par modèles délai, les modèles que
considèrent uniquement la taille des tâches et le délai de
communication entre tâches successives allouées à des
processeurs différents, lequel peut être aussi
considéré comme étant zéro.
Les modèles délai et des techniques
d'ordonnancement associés ont été proposés
simultanément. Pour ne pas anticiper la présentation de
l'ordonnancement, nous allons donner une description informelle. Un
ordonnancement d'un graphe sur une machine consiste à attribuer à
chaque tâche du graphe un processeur et une date de début
d'exécution.
Lors de la transmission ou de la réception d'un message
dans une machine réelle, le processeur est occupé pendant une
période de temps (avec des copies mémoire, allocation de tampons,
etc.). Les modèles de cette section ne prennent pas en compte cette
période sur le temps d'exécution des processeurs. Le recouvrement
total des communications par du calcul est autorisé, c'est-à-dire
que les processeurs peuvent calculer pendant les communications. Les
modèles délai ne prennent également pas en compte la
congestion du réseau. Le surcoût de communication sur le temps de
calcul et la congestion ont été considéré dans le
modèle LogP. Nous présentons d'abord le modèle avec bande
passante illimitée, c'est-à-dire, sans surcoût de
communication. Ensuite nous présentons les modèles avec bande
passante limitée, ce qui introduit des délais de communication.
Une des façons d'alléger ce surcoût peut se faire à
travers la duplication de tâches. Dans ce cas, nous pouvons au lieu de
communiquer à partir des prédécesseurs, dupliquer
quelques-uns d'entre eux. Les paramètres que nous utiliserons pour les
modèles suivants sont le nombre de processeurs et la possibilité
de dupliquer des tâches.
Nous présentons des exemples d'exécution du
graphe G de la figure II.4 sous les différents modèles
d'exécution. La représentation utilisée est le diagramme
de Gantt (diagramme espace temps classique où l'espace correspond
à l'occupation des processeurs) où les tâches, les
communications et les temps d'attente sont placés selon leurs dates,
processeurs et durées d'exécution. Le poids des sommets du graphe
G sont identiques, le poids de ses arcs sera explicité pour chaque
modèle.
3.2.1 Modèle UET Le modèle
L'approche théorique de base est simplement d'ignorer
le temps de communication entre processeurs. La bande passante est
considérée illimitée. Le modèle UET (unit
execution time) a été proposé par Papadimitriou et
Ullman [22]. Le temps d'exécution des tâches est unitaire, les
attentes dues aux communications ne sont pas considérées. Il est
clair que dans ce cas la duplication de tâches s'avère inutile. Ce
modèle est similaire au modèle PRAM.
Ordonnancement avec UET
Dans le diagramme de la figure II.9, nous présentons un
schéma d'exécution optimal. Les zones rayées correspondent
au temps d'inactivité, cette notion sera utilisée
dorénavant. L'ordonnancement est valide si la contrainte de
précédence est vérifiée. Au temps t = 0,
on place les tâches sans prédécesseurs directs v1
et v2 sur des processeurs libres p1 et p2. A ce
moment, un processeur sera inactif. Au temps t = 1, étant
donné qu'il n y a que 3 processeurs disponibles , on va donc choisir et
placer les tâches v3, v5, v4 sur les
processeurs. L'ordre importe peu car ils ont le même temps
d'exécution et le temps de communication est nul. Au temps t =
2, on choisit v6 qui n'était pas encore allouée et aussi
les tâches v5 et v7 sur les 3 processeurs. Au temps
t = 3, on place les trois dernières tâches
v11, v9, v10. On
remarque bel et bien que cet ordonnancement est valide et optimal car le temps
d'exécution est de 4 qui est presque égal au nombre de
tâches divisé par le nombre de processeurs = 11/3.
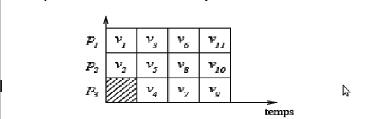
Figure II.9 - Exécution dans le
modèle UET
3.2.2 Modèle UET-UCT
Le modèle
L'extension naturelle du modèle UET considère de
manière simplifiée les communications. Lorsque les temps
d'exécution des tâches ainsi que les temps de communication sont
unitaires, nous avons le modèle UET-UCT (unit execution time -
unit communication time). Ce modèle a été
proposé par Rayward-Smith [28]. Les schémas d'exécution
avec et sans duplication sont représentés dans la Figure
II.10.
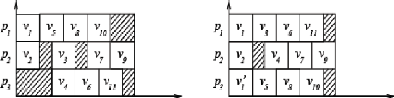
Dans l'exemple de la figure II.10, en permettant la
duplication, le temps d'exécution a été diminué
d'une unité. Dans la figure II.10 et dorénavant, lorsqu'une
tâche est exécutée plusieurs fois, une de ses allocations
est dénommée par l'index de la tâche. Les autres
exécutions d'une tâche v sont désignées par
v0 .
Ordonnancement avec UET-UCT
Ici l'idée est de chercher à placer les
tâches qui communiquent sur le même processeur pour annuler le
temps de communication.
Sans duplication : Au temps t
= 1, on place les tâches sans prédécesseurs
v1 et v2 sur p1 et p2 respectivement.
p3 est à ce moment inutilisé. Au temps t = 2,
on place les tâches v5 et v6 sur p1 et
p2 respectivement car v5 communique avec v1 et
v6 avec v2. p3 est toujours inutilisé. Au
temps t = 3, on place v4 sur p3 ( v1 a
terminé son exécution plus le temps de communication entre
p1 et p3.) Avec le même principe, on parcourt toutes
les tâches avec un temps de 6. On remarque que p3 passe beaucoup
de temps inactif.
Avec duplication : La tâche
v1 a été dupliquée sur p2 et p3
pour pouvoir placer v4, v5, v3 au même
moment.
3.2.3 Modèle UET-LCT Le modèle
Le modèle proposé par Papadimitriou et
Yannakakis [23] considère toujours des tâches de durée
unitaire, mais le coût de communication est donné par 'y >
1. Ce modèle est dénommé UET-LCT (unit
execution time - large communication time). Ce modèle convient
aux réseaux d'ordinateurs où les processeurs sont rapides et le
réseau représente le point d'étranglement du
système.

Figure II.10 - Exécution dans le
modèle UET-UCT sans et avec duplication
Ordonnancement avec UET-LCT
Dans la figure II-10, le temps de communication entre
tâches exécutées sur processeurs distincts est de 2,
5, c'est-à-dire deux fois et demi le temps d'exécution d'une
tâche.
Sans duplication : Au temps t
= 0, v1 et v2 sont allouées aux processeurs
p1 et p2.
Au temps t = 1, on choisit d'allouer v3,
v6 et v5 aux processeurs p1, p2 et
p3 ainsi les temps de communication entre v1 et v3 ,
v2 et v6 sont annulés. Tandis que v5
débutera son exécution au temps t = 1 + 1 + 2,
5 = 4, 5 puisqu'il s'exécute sur un processeur
différent de son prédécesseur direct.
Au temps t = 2, on choisit d'allouer v4
à p1.
Au temps t = 3, on alloue v7 sur le même
processeur que v3 et v4 annulant ainsi les temps de
communication.
Au temps t = 4.5, étant donné que
les tâches v7 et v5 ont déjà
terminées leur exécution, on choisit de lancer v9 sur
p1. Il débutera au temps t = 4,5 +
2,5 = 7.
On applique le même principe aux autres tâches.On
remarque que p2 est inactif longtemps.
Avec duplication : La tâche
v1 uniquement est dupliquée sur p2 pour pouvoir lancer
les tâches v3, v5 et v6 au temps 1. Egalement,
on a dupliqué v1 et v5 sur p3 pour pouvoir
lancer v11 tôt. v9 débute son
exécution au temps t = 4, 5 sur p1 puisque la
tâche v5 a terminé au temps 2 et v7 a
été exécuté sur p1.
On obtient un temps de t = 5,5 au lieu de t
= 8 sans duplication.

Figure II.11 - Exécution dans le
modèle UET-LCT sans et avec duplication
Jusqu'ici, les coûts des tâches ainsi que les
coûts des communications ont été constants. Il existe aussi
la possibilité d'avoir des coûts variables.
3.2.4 Modèle SCT Le modèle
Il existe d'autres approches telles que le modèle SCT
(small communication time) proposé par Colin et Chrétienne [7].
Dans ce cas, les temps d'exécution sont plus grands que les temps de
communication.
Ordonnancement avec SCT
La figure II-12 montre des schémas d'exécution du
graphe G avec et sans duplication. Le temps de communication est la
moitié de la durée d'une tâche.
Sans duplication : Avec un raisonnement
similaire à celui appliqué au modèle
précédent, on obtient un temps égal à 5 sans
duplication de tâches.
Avec duplication : On choisit de
dupliquer la tâche v1 sur p3 pour pouvoir
débuter v3 plutôt et réduire les temps
d'inactivité de p3. On obtient un temps de t = 4,
5.


Figure II.12 - Exécutions dans le
modèle SCT sans et avec duplication
L'intérêt de l'introduction de plusieurs
restrictions sur les modèles délai réside dans la
possibilité de pouvoir donner des garanties de performances plus fines
pour les problèmes d'ordonnancement.
3.3 Le modèle LogP Le modèle
Le modèle LogP [9] a le mérite d'avoir
été conçu conjointement par des spécialistes en
architectures, en environnements d'exécution et en algorithmique. Ce
modèle suppose un nombre fini P de processeurs à mémoire
locale. La topologie du réseau n'est pas prise en compte. Les
synchronisations sont faites par échange de messages. Le temps de
communication considère le coût d'échanges de message pour
chaque processeur. Dans le modèle LogP, les coûts de communication
sont déterminés à travers les paramètres L, o
et g.
Lors de l'envoi d'un message le processeur expéditeur
ne peut pas calculer pendant un période de temps, ce surcoût est
dénoté par o (overhead). La réception d'un
message coûte aussi un temps de calcul o du processeur
récepteur.
Il existe aussi un intervalle de temps minimal entre l'envoi
de deux messages par le même processeur, cet intervalle est
dénoté par g (gap). Cet intervalle de temps doit aussi
être respecté lors de la réception des messages.

Figure II.13 - Exemple des paramètres
LogP
La latence L(latency) est le maximum entre le temps
d'envoi d'un message (achèvement de l'opération d'envoi) et le
temps de réception de ce message (début de l'opération de
réception), sur des conditions de communication normales.
Pour éviter la congestion du réseau, au plus
partie supérieure de L/g messages peuvent transiter
simultanément. Dans la Figure II.13 nous illustrons les
paramètres du modèle LogP, "les tâches noires" sont dues
aux surcoûts de transmission et de réception. Un carré gris
représente la latence. Entre deux communications consécutives il
existe un intervalle de taille au moins g. La définition première
de LogP a été donnée pour de petits messages.
Avec de gros messages, la latence peut devenir
négative, le premier mot du message peut arriver avant le départ
de son dernier mot. Quelques variations plus générales du
modèle LogP ont été proposées par Hwang et al. [2,
11].
Ordonnancement avec LogP
La figure II-14 exhibe deux ordonnancements sous le
modèle LogP sans duplication. Dans le premier (à gauche) o
= 0, 125 et L = 0, 25 du temps
d'exécution d'une tâche, le paramètre g est au
plus 1. Dans le deuxième exemple (à droite) nous utilisons les
mêmes valeurs pour o et L cependant g =
1.5.
Dans le premier cas, on choisit d'ordonnancer v1 et
v2 sur les processeurs p1 et p2 respectivement.
v5 débute son exécution au temps t = 1 + 0,
125 puisqu'il utilise un surcoût de 0, 125 pour l'envoi du
message à v3.
La tâche v6 débute au temps 1. La
tâche v11 débutera au temps t = 1 +
0, 125 + 1 + 0, 125 + 0, 25 + 0, 125 =
2, 625 tenant en compte le temps de transmission du message venant de
v5, le temps de traitement de l'envoi par v5 et le temps
traitement de la réception par v11. v3
débute à son tour sur p3 au temps t = 1 +0,
125 +0, 25 +0, 125 = 2 tenant en compte le temps de
transmission du message, le temps de traitement de l'envoi par v1 et
le temps de traitement de réception du message par v3. Les
tâches v4, v7 et v9 sont allouées au
processeur p3 mais la dernière devra traiter la
réception du message de v5 au coût 0, 125.
v8 et v10 sont allouées à
p1.
La figure de droite s'explique pareillement à la seule
différence qu'il faut considérer g = 1, 5.
3.4 Le modèle BSP Le modèle
Plus qu'un modèle d'exécution, BSP [15, 18, 30]
(Bulk Synchronous Parallel) est un modèle de programmation. Son
objectif est de fournir un cadre permettant de concevoir facilement des
algorithmes portables et efficaces. Le modèle BSP n'est pas basé
sur des modèles de machines existantes,

Figure II.14 - Ordonnancement sous le
modèle LogP
mais il convient aux machines MIMD. L'idée principale
du modèle BSP est la séparation du calcul de la communication.
Ses concepts de base sont la super-étape (de l'anglais super-step) et la
synchronisation.
L'application est divisée en super-étapes. Tous
les processeurs commencent une super-étape au même instant. Entre
deux super-étapes, il existe une étape de synchronisation. Les
données communiquées lors d'une super-étape seront
disponibles aux processeurs destinataires au début de la
super-étape suivante.
Les trois paramètres utilisés afin de
décrire le modèle sont p, l et g. Nous
utilisons les mêmes notations que celles utilisées dans [18],
malgré l'utilisation de g auparavant pour la description du
modèle LogP. Ce choix est motivé par la standardisation de ces
notations pour les deux modèles. p le nombre de processeurs de
la machine; l le coût d'une synchronisation globale; g
le temps de transport d'un mot par le réseau. Autrement dit, 1/g
est la bande passante. Le modèle original proposé par Valiant
[30] introduit un paramètre qui représente la
périodicité d'une synchronisation. Dans son modèle, une
vérification globale est effectuée après chaque
période de L unités de temps. Elle sert à
déterminer si la super-étape a été achevée
sur tous les processeurs. Dans la version du modèle
présentée par McColl [28] il n'y a pas de référence
à la périodicité. Cette approche a été
probablement choisie parce que dans les machines courantes la
périodicité peut être aussi petite que le coût de
synchronisation. C'est cette approche que nous avons adoptée dans ce
document. Pour pouvoir estimer le temps d'une application BSP nous introduisons
les terminologies suivantes :
- pi processeurs de la machine (0 i < p);
- Wis coût des calculs
exécutés par le processeur pi au cours de la
super-étape s;
- hs i - désigne le maximum du nombre de mots
reçus (ou envoyés) par le processeur pi au cours de la
super-étape s.
Une h-relation est une opération
d'échanges de données point à point entre les processeurs,
où chaque processeur peut envoyer et recevoir au plus h mots.
L'estimation du temps total d'un programme BSP est obtenue en sommant les temps
de ses super-étapes. Les démarches pour obtenir une application
efficace dans le modèle BSP sont donc : équilibrer la charge de
calcul entre les processeurs au cours de chaque super-étape,
équilibrer les communications au cours d'une super-étape
(éviter les congestions) et finalement minimiser le nombre de
super-étapes.
Pour les schémas d'exécution dans le
modèle BSP nous avons choisi une représentation explicite des
communications entre les processeurs (figure II-15 à gauche)2
et représentation implicite des communications entre les processeurs
entre les super-étapes. Les communications entre les processeurs sont
représentés comme une barrière grise ( correspondant
à la h-relation ) qui se trouve juste avant la synchronisation (
barrière noire dans la figure II-15 à droite ). De cette
façon les communications
2Les flèches représentent les
données envoyées d'un processeur à l'autre
restent implicites3. Ordonnancement avec
BSP
Dans l'exemple, le temps pour achever une h-relation est 0,5 du
temps d'exécution d'une tâche. Le temps de synchronisation est
0,25.
On alloue les tâches v1 et v2 aux
processeurs p1 et p2. On choisit d'exécuter les
tâches v3, v5, v6 sur les processeurs
p1, p2, p3 respectivement.
Dès que les tâches v1 et v2 ont
terminées leur exécution, une h-relation est effectuée
puisque les données doivent être transmises de p1
à p2, de p2 à p3.
Tous les processeurs vont donc débuter cette
super-étape. Elle sera suivie par une étape de synchronisation
pour s'assurer que les processeurs ont terminés les communications au
même instant. Egalement, il y aura une h-relation après
l'exécution des tâches v7 et v10 pour
pouvoir transférer les données entre les processeurs.
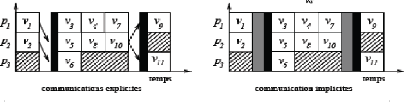
Figure II.15 - Schéma
d'exécution dans le modèle BSP
| 


