Conception et realisation d'un sechoir a condensation pour fruits et legumes

II. ELABORATION DES MODELES DE CALCUL

Le dimensionnement des différents systèmes ne peut se faire que si les principaux paramètres thermiques sont maîtrisés dans le séchoir. Pour y parvenir, il faut donc élaborer des modèles de calcul pour prédire l'évolution de ces paramètres. C'est ce qui est fait dans cette section. Nous devons donc modéliser les transformations subies par l'air humide à la traversée de chaque système (voir figures 2 et 3 pour mémoire).

1. Quelques notions fondamentales sur le séchage

· Eau libre : tout produit à sécher est poreux. Il existe dans le produit de l'eau sous forme liquide piégée dans les pores par capillarité, c'est l'eau libre ;

· Eau liée : grâce aux propriétés hydrophiles du produit à sécher, une portion d'eau se retrouvera sur et dans les parois des pores (on parle alors d'adsorption). C'est l'eau liée ;

· Flux-masse : c'est la masse d'eau évaporée par unité de surface d'échange du produit et par unité de temps. Elle sera notée par la suite Fm ;

· Teneur en eau base sèche du produit : noté W, et définie par

W = Masse d'eau dans le produit Masse de produit sec

· Porosité d'un amas de produit : notée å, elle vaut

å = Volume de l'amas - Volume du produit Volume de l'amas

· Compacité d'un amas de produit : noté á, elle vaut

á = Surface d'échanges convectifs Volume de l'amas

· Compacité base sèche d'un produit : elle est définies par

ás = Surface d'échanges convectifs sur le produit
Volume sec du produit

N.B. : Dans la définition des compacités, il s'agit d'échanges convectifs de chaleur et de masse.

2. Les différentes phases de séchage

On distingue 4 principales phases lors du séchage d'un corps hygroscopique, ce qui est le cas des denrées à sécher.

· Une période de préchauffage : elle correspond à la montée en température du produit, jusqu'à atteindre la température de bulbe humide caractéristique de l'environnement séchant. Cette période est généralement très courte au regard du temps de séchage global. C'est pourquoi nous ne la prendrons pas en compte dans les dimensionnement ;

· Une période à vitesse constante : ici, l'eau libre est éliminée à flux-masse constant. Elle est généralement isenthalpe. L'évaporation s'effectue à la surface du matériaux, à la température de bulbe humide de l'environnement séchant. Dans cette phase la température reste constante, car toute la chaleur apportée est utilisée pour l'évaporation. Cette phase est la plus exigeante d'un point de vue énergétique. C'est pourquoi c'est elle qui sera modélisée pour les dimensionnements.

· Une première période de ralentissement : elle commence quand le font d'évaporation, qui se trouvait à la surface du produit, se déplace vers l'intérieur. Là commence alors une migration d'eau liée, en plus de celle d'eau libre.

· Une seconde période de ralentissement : le flux-masse décroît plus rapidement que précédemment. Ici, l'eau libre est finie et il ne reste plus que l'eau liée qui sera évacuée très lentement par le phénomène de diffusion-sorption.

Par OUAMBO. R et DJUIKAM M.F.H.M. ENSAI de Ngaoundéré, février 2003. 21

3. Equations des bilans dans le compartiment de séchage

Ces équations décrivent l'évolution des paramètres d'air humide et du produit à la traversée d'une claie grillagée, pendant un temps At. Elles sont issues de la référence [6]. Les hypothèses sont les suivantes :

· Les variations d'humidité absolue et de température de l'air sont unidirectionnelles et spatiales uniquement ;

· La variation de teneur en eau base sèche des produits est uniquement temporelle ;

· La vitesse de l'air est constante dans tout le compartiment de séchage ;

· Les déperditions à travers les parois sont négligées en première approximation ;

· L'ambiance de séchage est non rayonnante ;

· Les propriétés physiques du produit et de l'air humide sont supposées constantes ;

· L'influence de la teneur en eau de l'air sur sa chaleur massique est négligée ;

· Le produit est en phase isenthalpe (sa température reste constante).

Bilan de masse sur le produit

^a Ä

s W = - F m

ñ

á Ä t

s

Bilan de masse sur l'air

Ä W

ñ a 8

U =F

8 m

Ä z

å

1 - å

á

Bilan d'énergie sur le produit

h · ( T 8 - T) = ÄH _v ·Fm

å

1

-

å

ñ_a

á

8

Cp_aU = · -

h T T (

8 8

Ä

z

ÄT

)

Bilan d'énergie sur l'air

· a

ñ_s est la masse volumique apparente du produit sec.

· ñ_a est la masse volumique de l'air sec. Elle dépend de la température (voir [6]) ;

· U₈ est la vitesse de l'air de séchage ;

· W₈ est l'humidité absolue de l'air humide de séchage ;

· T₈ est la température de l'air humide de séchage ;

· T est la température du produit ;

· h est le coefficient d'échange convectif à la surface du produit. On là supposé
identique à celui d'une plaque plane traversée par un courant d'air de vitesse U₈

· Cp_s est la chaleur massique du produit sec ;

· Cp_a est la chaleur massique de l'air sec, et vaut 1.006 KJ/Kg °C ;

· Pour un produit découpé en lamelles comme les mangues d'épaisseur e, on a 2

á =

e

4. Modélisation de la traversée de l'évaporateur (batterie froide)

Ici, l'air humide subira un refroidissement avec condensation. L'évolution est celle décrite dans la figure suivante.

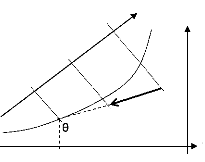
h1

w

h2

hè

1

2

t

èe

h

Figure 6 : Evolution de l'air sur la batterie froide

èe est la température moyenne de surface de l'évaporateur. Le problème ici est de trouver w2 et t2 en fonction de w1 et t1. Pour cela, nous utiliserons les deux équations suivantes :

· L'efficacité de la batterie (chaleur échangée sur le maximum échangeable) est

ç =

h h

1 - è

h h

1 - 2 et est de l'ordre de 0.7 ;

· Les points 1, 2 et è sont situés sur la même droite :

-

w w

-

1 2

w_è

w 1

.

t₁

-

-

t₁

t_è

t 2

Ce sont ses deux équations qui ont été utilisés dans le code de simulation donné dans l'annexe 3.

5. Modélisation du préchauffage sur le compresseur

Le compresseur n'a pas encore été sélectionné. Néanmoins, à partir de l'analyse fonctionnelle, on sait qu'il sera hermétique à piston, et que sa puissance n'excédera pas 2 KW. Nous ferrons donc nos estimations préliminaires sur les bases ci-après :

· Compresseur de puissance 1.5 KW et de rendement effectif 0.7 ;

· Toutes les pertes sont transformées en chaleur ;

· Les déperditions à travers les parois sont négligées dans ce compartiment.

·

m

1

2

·

m

·

m · h - h = - eff ·

( 2 1 ) (1 ç )

Le bilan d'enthalpie donne alors :

6. Modélisation de la traversée du condenseur (batterie chaude)

A la traversée du condenseur, l'air humide subit un échauffement simple, décrit dans la figure suivante.

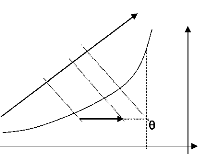
w

hè

h2

h1

1 2

t

èc

h

Figure 7 : Evolution de l'air sur la batterie chaude

èc est la température moyenne de surface du condenseur. Les 2 équations à prendre en compte ici sont :

· w₂ = w₁

· L'efficacité de la batterie (chaleur échangée sur le maximum échangeable) est h h

-

2 1

ç = et est de l'ordre de 0.7.

h h

-

è 1

Ce sont ses deux équations qui ont été utilisés dans le code de simulation donné dans l'annexe 3.