1.3. ANALYSES STATISTIQUES
La saisie des données et les calculs statistiques ont
été effectués à l'aide d'un micro-ordinateur de
marque Zenith IBM compatible. Le logiciel DBase III Plus a servi à la
saisie des données, le SPSS PC à l'analyse statistique et le 2L
BMDP à l'estimation de Kaplan-Maier et au modèle de COX.
L'analyse descriptive a été
réalisée grâce aux calculs des proportions, des moyennes,
des médianes, l'intervalle de confiance à 95% et des
écart-types. Pour l'analyse inférentielle, le test de T-student
et le test U de Mann-Whitney ont été utilisés pour
comparer les moyennes, le test Chi-carré pour comparer les proportions
et l'analyse des variances pour comparer les données
métriques.
Les mesures tensionnelles et
écho-vélocimétriques effectuées de manière
répétitive ont exigé de corriger les tests de Student par
la méthode de Bonferonni pour comparer les groupes entre eux. Si
l'effectif est inférieur à 20, la correction de Yates a
été appliquée pour utiliser le test Chi-carré
(Chi-Deux).
L'évaluation de la liaison entre variables
métriques s'est faite par le calcul du coefficient de
corrrélation linéaire de BRAVAIS-PEARSON.
Les statistiques de survie ont évalué le
pronostic de l'infection VIH par le calcul des taux de mortalité ou de
survie (probabilité) avec la méthode des estimateurs de
Kaplan-Maier. La régression de Cox a estimé de façon
quantitative l'effet d'un paramètre extérieur (facteur de
pronostic) sur la survie. Pour pouvoir tenir compte de la totalité de
la courbe de survie et des données tronquées (censurées ou
censored) pouvant biaiser les moyennes de survie, les groupes ont
été comparés par le test du logrank (équivalent du
test de Student pour des données censurées). Ce modèle de
régression très général a été
proposé en 1972 par Cox (COX D.R., 1972) à travers les relations
suivantes :
- 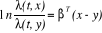
où xT = (x1, x2,
...xp) et yT = (y1, y2, ...
yp)
p facteurs de risques (covariables), ë(t, x) fonction de
survie
- ou bien
F(t ; Z) = [ Fo(t) ]exp (zâ)
F(t ; Z) fonction de survie ; Fo(t) valeur de la
fonction de survie pour une valeur nulle de la variable indépendante
Z.
Les tests statistiques ont porté sur le coefficient
â. Ce modèle est connu sous le nom de "modèle des risques
proportionnels parce qu'il suppose que les variables indépendantes
agissent de façon multiplicative sur la fonction de survie. Le rapport
RR (pour Z=0 du facteur de risque, et Z = 1 du même facteur) est le
risque relatif de mortalité. La méthode "pas-à-pas"
(stepwise) pour le modèle de Cox a été utilisée
pour ne retenir que les variables les plus significatives.
Les seuils de signification ont été
utilisés selon les valeurs de p suivantes :
- p 0,05 : non significatif (NS)
- 0,01 p 0,05 : significatif (*)
- 0,001 p 0,01 : hautement significatif (**)
- p 0,001 : très hautement significatif (***).
| 


