Essai de modélisation de l'inflation en Algerie

Chapitre IV

APPLICATION DES METHODES

CITEES

Section 1 : METHODE DE BOX & JENKINS

10

8 6 4 2 0

- 2 -4

- 6

INFLATION

1990 1992 1994 1996 1998 2000 2002 2004 2006

L'examen du graphique fait apparaître une tendance approximativement linéaire et, vraisemblablement, il sera nécessaire de différencier la série brute.

Test de saisonnalité et de tendance sur l'inflation (test ANO VA) (1) : H0 : pas d'influence.

ANALYSE DE VARIANCE

Source des variations Somme des carrés Degré de libertéMoyenne des carrés F Valeur critique pour F

Lignes	170.4075684	16	10.65047303 5.29314	1.70126313
Colonnes	290.5360813	11	26.41237103 13.1266	1.843392994
Erreur	354.1343201	176	2.012126819
Total	815.0779698	203

Effet ligne : 5.3 > 1.70. On rejette H0, la série est donc affectée d'une tendance.

Effet colonne : 13.12 > 1.84. On rejette H0, la série est donc affectée d'une saisonnalité.

Donc présence de saisonnalité et de tendance.

(1) Test fait sur Excel, suivant ces différentes étapes :

1) Construire le tableau de Buys-Ballot (tableau croisé).

2) Faire: outils> utilitaire d'analyse> analyse de variance.

La fonction d'autocorrélation estimée est nettement positive pour les premières valeurs (tendance) ; et on remarque des pics significatifs pour les retards multiples de 12 (saisonnalité).

Test de racine unitaire ADF : Avec un maximum Lags=10 pour le critère de Schwartz (sous Eviews 5.1 le choix des retards pour l'application du test de Dickey-Fuller est automatique, le logiciel choisi le modèle pour lequel le critère de Schwartz est le minimum).

Modèle 3 :

La réalisation de la statistique de Student est égale à -15.82, on compare cette valeur aux seuils de la table de Dickey-Fuller tabulés par MacKinnon pour le modèle 3 et pour une taille d'échantillon de 203 observations. Au seuil de 5%, le seuil critique est - 3.43. Ainsi on rejette l'hypothèse nulle de racine unitaire. Par contre, le coefficient de la tendance est significativement différent de 0, on confirme la présence d'une tendance.

On applique la différenciation première pour éliminer la tendance, on aura la série y_t = inflation (t)-inflation (t-1) et une moyenne mobile d'ordre 12 sur la série y_t (qui suit un modèle additif)⁽¹⁾ pour éliminer la saisonnalité. Soit X_t notre nouvelle série.

Nous allons travailler sur la série X_t :

8

4

0

-4

-8

1990 1992 1994 1996 1998 2000 2002 2004 2006

x

(1) Nous avons appliqué "le test de la bande", qui consiste à relier par une ligne brisée toutes les valeurs hautes et les valeurs basses de la chronique. Et on trouve qu'elles sont approximativement parallèles, caractéristique d'un modèle additif.

Le corrélogramme de la série X_t ne présente plus systématiquement de fortes valeurs des autocorrélations pour les premiers retards ou pour les retards multiples de 12. On peut donc considérer que la série X_t a été générée par un processus stationnaire. Cependant, on remarque des pics dispersés (12, 13, 25,35) qui peuvent apparaître non nulles, nous allons générer une nouvelle série par une interpolation sur la serie X_t, de façon à éliminer ces pics.

Nous allons travailler sur la série X_t après transformation :

D'après le corrélogramme de X_t on remarque que les 4 premiers retards de l'autocorrélation partielle décroissent de façon exponentielle et sont significatifs, ainsi que le premier retard de l'autocorrélation.

Nous allons modéliser cette série (X_t) par un processus ARMA Test de différents modèles :

A) Modélisation à l'aide d'un MA (1) :

Le corrélogramme de X_t fait apparaître les caractéristiques d'une moyenne mobile d'ordre un, Il peut être intéressant de considérer un modèle de type MA (1) sur cette série (respectivement avec et sans constante),

· Avec constante :

· Sans constante :

Les résidus, représentés ci-dessous à gauche, ont le corrélogramme suivant

6 4 2 0 -2 -4 -6

8 4 0 -4 -8

1990 1992 1994 1996 1998 2000 2002 2004 2006

Residual Actual Fitted

Le modèle présenté est candidat : le coefficient est significatif, et les erreurs suivent un bruit blanc.

B) Modélisation à l'aide d'un ARMA (4,1) :

Les 4 premières autocorrélations de (X_t) sont significativement non nulles : ceci pousse à tester un modèle ARMA (4,1), soit

·

· Sans constante :

dont les résidus ont le comportement suivant :

6 4 2 0 -2 -4 -6

1990 1992 1994 1996 1998 2000 2002 2004 2006

Residual Actual Fitted

8 4 0 -4 -8

Avec constante :

On peut noter que tous les retards semblent significatifs, et les erreurs suivent un bruit blanc, donc le modèle est candidat.

C) Choix du modèle :

Modèles	ó	Critère d'Akaike	Critère de Schwarz
MA (1)	1.365	3.466	3.482
ARMA (4,1)	1.249	3.318	3.417

Le processus ARMA (4,1) est le modèle choisi, car il minimise tous les critères. Tests sur les résidus du processus ARMA (4,1) :

· La statistique de Durbin-Watson est proche de 2, donc absence d'autocorrélation d'ordre 1.

· Le test de Ljung et Box⁽¹⁾ L'hypothèse à tester est H0 : « les résidus sont non corrélés »

Q12 =	2 12.52< X 12 (0.95)	=		21.03	Q24 =
2 26.32< X 24(0.95)	=	36.42		Q37 =
2 41.18< X 37 (0.95)	=	55.76

Dans tous les cas l'hypothèse H0 est acceptée, on confirme donc que les résidus forment un bruit blanc.

· Statistique descriptive des résidus

Series: Residuals

Sample 1990M06 2006M12 Observations 199

Mean -0.017594

Median -0.009316

Maximum 4.862647

Minimum -4.142255

Std. Dev. 1.236973

Skewness 0.179849

Kurtosis 4.850210

Jarque-Bera 29 .45748

Probability 0.000000

30 25 20 15 10 5 0
-2.5 0.0 2.5 5.0

(1) La statistique Ljung-Box correspond à la statistique Q-stat sur le corrélogramme d'Eviews

·

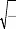
Test de nullité de la moyenne des résidus : (test t et test z)

:0 ì =

:0

ì ?

? H0

?? vs

? ? H1

On a la probabilité > 0.05 pour les deux tests, donc on accepte au seuil 5% l'hypothèse H0 de nullité de la moyenne.

· Test de Jarque-Bera (normalité) : L'hypothèse à tester est H0 : << les résidus suivent une loi normale >> au seuil de 5%

H0 : << ã ₁ =0,ã₂ =0 >> contre H1 : << ã 1 ? 0,ã₂ ? 0 >>

1

s 2 -

ã= = <1.96 : on accepte l'hypothèse de symétrie

0 1.035

2 6

n

- 3 5.327
=

24

n

k

ã₂

>1.96 : on rejette l'hypothèse d'aplatissement, la Kurtosis excède 3

(queues épaisses).

Pour le test de Jarque-Bera on a : Probabilité = 0.000 donc on refuse l'hypothèse H0 de normalité des résidus.

· Test d'homoscédasticité (test de White) : H0: << les résidus sont homoscédastiques >>

2 2

On a : TR12.38 ₈ (0.95)15.51

=< ÷ = , donc on accepte l'hypothèse H0 d'homoscédasticité.

Conclusion, le meilleur processus qui ajuste la serie X_t est un ARMA (4.1), qui s'écrit comme suit :

(11.2070.8180.6160.317) _t (10.55) +L+L+L+LX =+Lå _t

23 4

Ce modèle peut alors être utilisé pour faire de la prévision. Sous Eviews, nous obtenons les prévisions suivantes, sur 12 mois, pour X_t

h	1	2 3	4	5	6	7	8	9	10	11	12
x à( h ) ó	-0.7 19 1.254	-0.035 -0.309 1.508 1.51	0.243 1.511	0.2 107 1.523	-0.25 1 1.521	0.08 1.535	-0.097 1.536	0.140 1.537	-0.06 1.539	-0.008 1.5401	0.0032 1.54

4 3 2 1 0

- 1

- 2

- 3

-4

2007M01 2007M04 2007M07 2007M10

Prévision pour X Bornes de l'IC

Pour les prévision de la série inflation il est nécessaire de prendre en compte la transformation retenue et de »recolorer la prévision».

Dans ce cas la transformation est simple,

1. on ajoute les coefficients saisonniers à la série X_t pour avoir la série y_t et ses prévisions notées yà(h).

2. ensuite, on inverse le filtre d'ordre un sur la série y_t pour avoir la série initiale et ses prévisions notées ~ inf(h).

La série inflation peut être modélisé par un processus ARIMA (4, 1,1) saisonnier, qui s'écrit comme suit :

(1+1.207L+0.818L+0.616L+0.317L)(1-L)inf _t =(1+0.55L)å _t

2 3 4

On résume toutes les étapes précédentes dans le tableau suivant :

Mois	x à(t+h)		s(t)			yà(t+h)=xà(t+h)+s(t)		~inf(t+h)=yà(t+h)+ ~ inf(t+h-1)
Déc 06	1.90		-0.714			1.186		1.915
Jan 07	-0.719		1.108			0.389		2.304
Févr07	-0.035		-2.87			-2.905		-0.601
Mar 07	-0.309		1.818			1.509		0.908
Avr 07	0.243		-1.409			-1.166		-0.258
Mai 07	0.210		1.99			2.2		1.942
Juin 07	-0.251		-1.93			2.181		4.123
Juil 07	0.08		-1.51			-1.43		2.7
Aoû 07	-0.097		3.485			3.388		6.081
Sep 07	0.140		0.037			0.177		6.258
Oct 07	-0.06		-0.825			-0.885		5.373
Nov 07	-0.008		0.824			0.816		6.19
Déc 07	0.003		-0.714			-0.711		5.478
10 8 6 4 2 0 -2 -4 -6
		90 92 94 96 98 00 02 04 06
							Inflation Previsions

Section 2 : METHODE DE HOLT & WINTERS

A titre de comparaison nous allons calculer des prévisions pour la série inflation en utilisant la version additive du modèle de Holt Winters, avec les paramètres á ,â etã

estimés par le logiciel utilisé (1)

Optimal weights:	= = = = = =
alpha		0.0535
beta		0.0000
gamma		0.1046
penalized sum-of-squared residuals		433.8219
sum-of-squared residuals		433.8219
root mean squared error		1.458279

Les prévisions seront:

Jan 2007	1.599555
Fév 2007	-1.579485
Mars 2007	.3878582
Avr 2007	-.8518056
Mai 2007	.6688783
Juin 2007	-.9827 16
Juil 2007	-2.595066
Août 2007	.73040 16
Sept 2007	.9481627
Oct 2007	-.0745866
Nov 2007	.82133 14
Déc 2007	.2773956

Sous le logiciel STATA, l'estimation des paramètres par la méthode Holt & Winters est faite de façon à minimiser la somme carrée des résidus.

Les résultats montrent que le coefficient du lissage de la tendance est nul, alors que ceux de la moyenne et de la saisonnalité (respectivement 0.053 5 et 0.1046) sont proches de 0, ce qui prouve que la pondération s'étale sur un grand nombre de termes du passé, d'où la mémoire du phénomène étudié est forte et la prévision est peu réactive aux dernières observations.

(1) Pour cela nous avons utiliser le logiciel Stata.

Section 3 : COMPARAISON DES DEUX METHODES

Nous avons établit deux méthode de prévisions, il est évident de les comparer afin de les départager en matière de qualité prévisionnelle. En se basant sur des critères de mesure de la qualité de prévision décrite précédemment dans le chapitre 4, nous utiliserons le RMSE.

Méthode utilisée	RMSE
BOX & JENKINS	1.972
HOLT & WINTERS	1.459

Nous pouvons conclure que la méthode Holt & Winters fournit les meilleures prévisions puisqu'elle minimise le RMSE.

12

8

4

0

-4

-8

1990 1992 1994 1996 1998 2000 2002 2004 2006

Inflation ARMA Holt-Winters