Evaluation des performances d'un design d'avion de type blended-wing-body de 100 passagers

2.2.2.1. Estimation de la masse du fuselage

_{0,166552 1,061158}

_W = _{K x 0,316422} ? _{MTOW x S}

_{fuse s cabine}

Le modèle de Bradley (2004) a été utilisé pour prédire la masse du fuselage. La méthode de prédiction de masse de Bradley repose sur un modèle semi-empirique implémenté dans le logiciel d'optimisation de vol (FLOPS). Ce modèle permet de déterminer la masse du corps central d'un BWB comme étant la somme de la masse du corps central avant (qui représente la partie pressurisée du fuselage) et du corps central arrière compté à partir de 70% de la corde du corps centrale, tel qu'illustré par la figure 2.2.

_MTOW

K s = ( _{5,698869 450} ) n pax

Avec ce modèle, la masse du corps central avant est donnée comme suit :

(2.1)

Avec :

.

[lb] le poids total maximum au décollage.

26

[ft²] la surface de référence de la cabine. le nombre de passagers.

La masse du corps central arrière incluant un facteur pour le nombre de moteurs supportés par le corps central est donnée par l'équation suivante :

(2.2)

Avec :

le nombre de moteurs installés sur le fuselage.

[ft²] la surface de référence de la section arrière du fuselage.

[lb] le poids total maximum au décollage. l'effilement de la section arrière du fuselage.

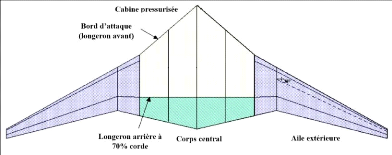
Figure 2.2 : Vue en plan de la géométrie simplifiée du BWB (Bradley, 2004)

2.2.2.2. Estimation de la masse de l'aile extérieure

Dans ce travail, l'aile extérieure du BWB sera assumée semblable à l'aile d'un avion conventionnelle. Dans la littérature, Il existe plusieurs modèles semi-empiriques permettant d'estimer la masse de l'aile d'un avion conventionnel, à l'instar des modèles de Howe (2000), de Kundu (2019) et de Torenbeek (2013).

27

· Avec le modèle de Howe, la masse de l'aile extérieure est donnée par l'équation suivante (Howe, 2000) :

[kg] (2.3)

Où :

est l'allongement de l'aile.

[m²] est la surface de référence de l'aile.

= 9x 10^-a pour les avions de type jet moyen-courrier.

est l'effilement de l'aile.

[m/s] est la vitesse de divergence de l'avion.

· Avec le modèle de Kundu, la masse de l'aile extérieure est donnée par l'équation

suivante (Kundu, 2019) :

_{W =c ?k ?k ?k ?k ?k} ?

_{wing w uc sl sp wl re}

( _{MTOW?nul)0,48?Sw,78?ARw?(1+?)0,4}

? ₁ - _{Wfuel _mass _in _wing}

? MTOW

		cos ( ) ? 0.25 ? t c		0,4

^re pour aucun moteur, 0,98 pour deux moteurs et 0,95 pour quatre moteurs (généralisé).

(2.4) Où :

_k=1

c_w = 0, 0215 pour des volets de montage standard sur l'aile.

k =1,02 pour le train d'atterrissage monté sur les ailes, sinon 1,0.

ksl =1,04 pour l'utilisation des slats.

ksp =1,01 pour un spoiler.

kwl =1,01pour un winglet (une approche généralisée consiste à avoir une taille standard).

· 28

_?V.

Avec le modèle de Torenbeek, la masse de l'aile extérieure est donnée par l'équation suivante (Torenbeek, 2013) :

Où :

_t c VT

(2.5)

[ft] une valeur de référence du modèle. [lbf/ft²] une valeur de référence du modèle.