4.2.1.2. Localisation des centres aérodynamiques
et
La figure 4.3 présente la position des centres
aérodynamiques du corps centrale et de l'aile extérieure, sur la
géométrie de l'avion.
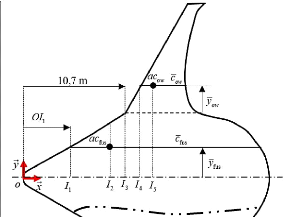
Figure 4.3 : Localisation des centres aérodynamiques du
corps central et de l'aile
97
1
(4.16)
La corde moyenne aérodynamique d'une aile
trapézoïdale est donnée par la relation
suivante (Corke, 2003) :
(4.11)
Où : et sont respectivement la corde à la racine et
l'effilement de l'aile.
La distance entre la corde moyenne aérodynamique de l'aile
et la corde à la racine est
donnée par la relation suivante (Corke, 2003) :
(4.12)
Où : est l'envergure de l'aile.
Par simplification, le centre aérodynamique d'une aile
est généralement pris au quart de sa corde aérodynamique
moyenne . Au regard de la géométrie de l'avion
présentée à la figure 4.3, la localisation des centres
aérodynamiques du corps central et de l'aile extérieure est
donnée par les relations géométriques suivantes :
X
fus =y ac fus tan ? LE
+c
,fus fus
(4.13)
(4.14)
En fonction des paramètres géométriques
des ailes complètes, les équations (4.13) et (4.14) deviennent
:
X ow = OI + y ow ?
LE ow + c ow
tan
ac 3 , 4
1
4
(4.15)
dCL
(4.18)
98
Où :
et sont respectivement les cordes moyennes aérodynamiques
du corps central et de
l'aile extérieure.
et sont respectivement les distances entre la corde à la
racine et la corde moyenne
aérodynamique, du corps central et de l'aile
extérieure.
et sont respectivement les angles de flèche au bord
d'attache du corps central et
de l'aile extérieure.
4.2.1.3. Détermination des coefficients de portance
du corps central et de l'aile
Le corps central est caractérisé par un profil
aérodynamique LA2573A. Comme énoncé dans les
hypothèses, nous assumerons que celui-ci s'étend
symétriquement des extrémités y = 0 m à y = 6,5 m
(c'est-à-dire jusqu'à la racine de l'aile extérieure).
L'aile extérieure quant à elle est caractérisée par
un profil aérodynamique SC(2)-0712 à ses extrémités
(y = 6,5 m et y = 17,2 m). Les coordonnées des points constituant les
profils du corps central et de l'aile extérieure sont
présentées dans l'annexe 3.
L'équation de la droite de portance d'une aile
tridimensionnelle (c'est-à-dire complète) est donnée par
la relation suivante (Anderson, 1999) :
(4.17)
Où :
est l'angle d'incidence du flux d'air avec le bord d'attaque de
l'aile (angle d'attaque) ; est l'angle d'attaque à portance nulle (c'est
le même en 2D qu'en 3D).
La théorie de la ligne de portance de Prandtl permet
d'estimer la pente de portance d'une
aile complète (Anderson, 1999). En vol subsonique
compressible, la pente de portance
pour une aile en flèche s'exprime comme suit (Anderson,
1999) :
CLa
= =
a A
0 cos 0.5
da 2
2
1 - M cos 2 A
+ ? A
( ) ( ) ? + ( ) ( )
0.5 ? a cos ?
AR
0 0.5 ? a cos A ?
AR
? 0 0.5
99
Où :
[rad-1] est la pente de portance du profil
d'aile.
est le nombre de Mach en vol subsonique.
L'angle de flèche à la moitié de la corde
est donné par l'équation qui suit :
(4.19)
| 


