Evaluation des performances d'un design d'avion de type blended-wing-body de 100 passagers

4.2. Point neutre et stabilité statique du BWB

Encore appelé foyer, le point neutre est le point par rapport auquel le moment des forces de portance (aile extérieure et corps central dans le cas du BWB) reste constant, quel que soit l'angle d'attaque. Pour un avion, la position du point neutre par rapport au centre de gravité influe directement sur la stabilité.

Dans toute cette section, les hypothèses suivantes seront considérées :

- L'avion vole en palier, les forces de trainée () et de poussée () sont égales ; - Les forces de trainée () et de poussée () ne créent pas de moment ;

- Les forces de portance du corps centrale ( ) et de l'aile ( ) sont verticales.

4.2.1. Détermination du point neutre du BWB

Comme dit plus haut, au point neutre, le moment des forces de portance reste constant quel que soit l'angle d'incidence de l'avion. La détermination de sa localisation est un préalable à l'étude de la stabilité statique de l'appareil.

4.2.1.1. Modélisation simplifiée de l'équilibre du BWB

La figure 4.2 présente une modélisation simplifiée du BWB, ainsi que les forces extérieures qui s'y exercent en vol en palier.

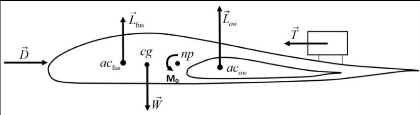
Figure 4.2 : Modèle simplifié du bilan des forces appliquées à un BWB

95

Sur cette figure, D représente le bilan des forces de trainée, T est la force de poussée totale des

moteurs, W est le poids total de l'avion appliqué au centre de gravité, est la résultante des
forces de portance générées par le fuselage (appliquée au centre aérodynamique du profil

d'aile) et est la résultante des forces de portance générées par l'aile extérieure (appliquée
au centre aérodynamique du profil d'aile également).

À l'équilibre, le bilan des forces donne :

? M _np ( L _fus ) M _np ( L _ow ) ₀

+ ? =

? ?

	(4.5)

Au point neutre, la somme des moments des forces aérodynamiques est constante, quel que soit l'angle d'attaque. Ceci se traduit analytiquement par l'équation suivante :

? ? _L X _np X ac L _ow X ac X np

? ( - ) ( )

- - ? = ₀

? fus

?? ?

(4.6)

(4.7)

Sachant que les forces aérodynamiques s'appliquant à l'avion ont pour résultante les forces de portance générées par le fuselage et l'aile extérieure, l'équation (4.7) implique :

² L OW = ? S _{OW V} C _{L OW
L} = ? _{S V} C L

_{fus fus ,fus} ,

_{2 2}

_S

_{S C S C}

_{fus L} , _ow

C _{L ,fus}

= C ow =

_Sa

_{L a L a}

_{Sa Sa}

_{1 1}

(4.8)

_fus

_ow

(4.9)

₂

Sachant que : et

Puis en posant : et

L'équation (4.9) permet de déduire la position du point neutre de l'avion :

96

(4.10)

Où :

est l'abscisse du point neutre par rapport au repère avion.

est l'abscisse du centre aérodynamique du corps central par rapport au repère avion.

est l'abscisse du centre aérodynamique de l'aile par rapport au repère avion.

est le coefficient de portance du corps central.

est le coefficient de portance de l'aile extérieure.

est la surface plan du corps central.

est la surface plan de l'aile extérieure.

Il ne reste plus qu'à déterminer chacun des paramètres de l'équation (4.10) pour trouver la position du point neutre.