Chapitre 2
Modélisation dynamique d'un
quadrotor
Chapitre II Modélisation dynamique d'un
quadrotor
16
Chapitre II : Modélisation dynamique d'un
quadrotor
II.1. Introduction :
Afin de concevoir un contrôleur de vol, on doit d'abord
comprendre profondément la dynamique de l'avion, par conséquent
son modèle dynamique. Cette compréhension est nécessaire
non simplement pour la conception du contrôleur, mais aussi pour
s'assurer que le comportement de véhicule est plus proche que possible
de la réalité lorsque la commande est appliquée.
Le quadrotor est classé dans la catégorie des
systèmes volants les plus complexes vu le nombre d'effets physiques qui
affectent sa dynamique à savoir les effets aérodynamiques, la
gravité, les effets gyroscopiques, les frottements et le moment
d'inertie. Cette complexité résulte essentiellement du fait que
l'expression de ces effets diffère pour chaque mode de vol. En effet les
modèles dynamiques du quadrotor proposés changent en fonction des
taches planifiées et en fonction des milieux de navigation
définis à priori par l'opérateur.
II.2. Modèle dynamique du quadrotor :
La modélisation des robots volant est une tâche
délicate puisque la dynamique du système est fortement non
linéaire et pleinement couplée. Afin de pouvoir comprendre au
mieux le modèle dynamique développé ci-dessous,
voilà les différentes hypothèses de travail :
· La structure du quadrotor est supposée rigide
et symétrique, ce qui induit que la matrice d'inertie sera
supposée diagonale,
· Les hélices sont supposées rigides pour
pouvoir négliger l'effet de leur déformation lors de la
rotation.
· Le centre de masse et l'origine du repère
lié à la structure coïncident.
· Les forces de portance et de traînée sont
proportionnelles aux carrés de la vitesse de rotation des rotors, ce qui
est une approximation très proche du comportement
aérodynamique.
Pour évaluer le modèle mathématique du
quadrotor on utilise deux repères, un repère fixe lié
à la terre Rb et un autre mobile Rm. Le passage entre
le repère mobile et le repère fixe est donné par une
matrice dite matrice de transformation T qui contient l'orientation et la
position de repère mobile par rapport au repère fixe. On choisit
la convention d'axes suivants :
Chapitre II Modélisation dynamique d'un
quadrotor
17
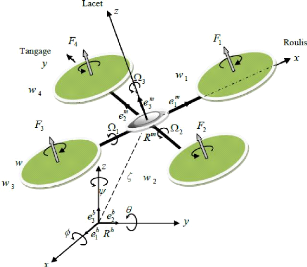
Figure 2.1 : Géométrie du quadrotor.
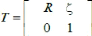
(1)
Avec R la matrice de rotation (décrit l'orientation de
l'objet mobile), æ = [x Y Z]T est le vecteur de
position. Pour déterminer les éléments de la matrice de
rotation R, on utilise les angles d'Euler.
II.2.1. Angle d'Euler :
Au début le repère mobile est coïncide avec
le repère fixe, après le repère mobile fait un mouvement
de rotation autour de l'axe x d'un angle de roulis(- 2 <
ç < 2), suivi d'une rotation
Autour de l'axe y d'un angle de tangage(- 2 <
ç < 2), suivi d'une rotation autour de l'axe z
d'angle de lacet(-7r < i < 7r). Donc on a la
formule de la matrice de rotation R :
ci -si 0 ce 0 se 1 0 0
R = Rots (i )
× Roty(e) × Rot,
(ç) = ~si ci 0 ~× ~0 1 0
~× ~0 cç-sç ~ (II.2)
0 0 1
-se 0 ce 0 sç cç
R = ~ci ce sçseci - sci ????
cçseci + si sç si ce sçsesi + ci ce
cçsesi - cçci ~ (II.3)
-se sçce
cçce
Avec : c = cos et s = sin
Chapitre II Modélisation dynamique d'un
quadrotor
II.2.2. Vitesses angulaires :
Les vitesses de rotations Ù1,
Ù2,Ù3dans le repère
fixe sont exprimées en fonction des vitesses de rotations ?????,
?????, ????? dans le repère mobile, on a :
Ù = ~Ù10
0
Ù2~ =
~?????0~ +
????????????????(????)-1
~????? ~+
(????????????????(????)????????????????(????))-1
~????0~ Ù3 0 0
|
(II.4)
|
|
En effet, la rotation en roulis a lieu lorsque les
repères sont encore confondus. Puis, en ce qui concerne le tangage, le
vecteur représentant la rotation doit être exprimé dans le
repère fixe: il est donc multiplié par
????????????????(????)-1. De
même, le vecteur représentant la rotation en lacet doit être
exprimé dans le repère fixe qui a déjà subites deux
rotations. On arrive ainsi à:
Ù???? ????? 0 -????????????? ????? -
?????????????
Ù = ~ Ù???? ~ =
~ ?????????????
0 ~ + ~ ~ + ~
????????????????????? ~ = ~ ????????????? +
????????????????????? ~ (II.5)
Ù???? 0 -?????????????
????????????????????? ????????????????????? - ?????????????
1 0 -????????
Ù = 0 ???????? ???????????????? ~
× ~(id (II.6)
0 -???????? ????????????????
Quand le quadrotor fait des petites rotations, on peut faire les
approximations suivantes:
cö =cè =cø =1, et sö =
sè = sø = 0.
Donc la vitesse angulaire sera:
Ù = [????? ????? ?????]
(II.7)
| 


