II.2.3. Vitesses linéaires :
Les vitesses linéaires ????????????,
????????????, ???????????? dans le repère fixe
en fonction des vitesses linéaires ???????????? ,
???????????? , ???????????? dans le repère
mobile sont données par :
18
???? ????
(II.8)
???????? ????????
???? = ~????????????~ = ????
× ~????????????~
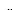
???? ????????

????????????
II.2.4. Effets physiques agissants sur le quadrotor :
II.2.4.1. Les forces :
Les forces agissant sur le système sont :
Le poids du quadrotor: il est donné par
P = mg, où : m est la masse totale et g la
gravité.
Chapitre II Modélisation dynamique d'un
quadrotor
19
Les forces de poussée: qui sont des
forces provoquées par la rotation des moteurs, elles sont
perpendiculaires sur le plan des hélices. Ces forces sont
proportionnelles au carrée de la vitesse de rotation des moteurs :
FL = bwL2 (II.9)
Avec i = 1: 4, et b est le coefficient de
portance, il dépend de la forme et le nombre des pales et la
densité de l'air.
Les forces de traînée : la force
de traînée est le couplage entre une force de pression et la force
de frottement visqueux, dans ce cas on a deux forces de traînée
agissant sur le système qu'elles sont :
· La traînée dans les hélices : elle
agisse sur les pales, elle est proportionnelle à la densité de
l'air, à la forme des pales et au carré de la vitesse de rotation
de l'hélice, elle est donnée par la relation suivante :
Th = dw2 (II.10)
Avec d est le coefficient de drag il dépend de
la fabrication de l'hélice.
· La traînée selon les axes (x, y,
z): elle est due au mouvement du corps du quadri-rotor
Ft = Kfty (II.11)
Avec : K ft le coefficient de
traînée de translation et V la vitesse
linéaire.
II.2.4.2. Les moments :
Il y a plusieurs moments agissants sur le quadrotor, ces moments
sont dus aux forces de poussée et de traînée et aux effets
gyroscopiques.
Moments dus aux forces de poussée :
· La rotation autour de l'axe x : elle est due au
moment crié par la différence entre les forces de portance des
rotors 2 et 4, ce moment est donné par la relation suivante :
Mx= l(F4 - F2) =
lb(w42 - w2 2) (II.12)
Avec l, est la longueur du bras entre le rotor et le
centre de gravité du quadrotor.
· La rotation autour de l'axe y : elle est due au moment
crié par la différence entre les forces de portance des rotors 1
et 3, ce moment est donné par la relation suivante :
My= l(F3 - F1) = lb(w32 -
w12) (II.13)
Moments dus aux forces de traînée
:
· La rotation autour de l'axe z : elle est due à un
couple réactif provoqué par les couples de traînée
dans chaque hélice, ce moment est donné par la relation suivante
:
Chapitre II Modélisation dynamique d'un
quadrotor
20
???????? = ????(????1 2 - ????2
2 + ????3 2 - ????42)
(II.14)
(II.15)
s Moment résultant des frottements
aérodynamiques, il est donné par :
???????? = ????????????Ù2
Avec ???????? ????: Le coefficient des frottements
aérodynamiques et ? est la vitesse angulaire.
| 


