CHAPITRE 2: Approche méthodologique
Le but de ce chapitre est d'expliciter les méthodes
statistiques auxquelles nous aurons recours pour l'atteinte de nos objectifs.
De ce fait, après une description préalable de la source des
données et de la zone d'étude, nous développerons la
méthode de détermination des facteurs influençant
négativement l'adoption des CES/DRS. Ensuite, nous procéderons
à la description de la méthode d'appréciation des effets
de cette adoption sur l'efficacité technique.
Source des données et zone d'étude Source
des données
Les données utilisées dans ce document sont
issues de l'Enquête Permanente Agricole (EPA) de la campagne 2015/2016.
L'Enquête Permanente Agricole est une enquête par sondage de
portée nationale. Elle couvre les 45 provinces du pays selon le
découpage administratif et a principalement pour objectif de:
· estimer les productions et les rendements de
l'ensemble des 45 provinces du pays pour chaque culture ;
· estimer les superficies emblavées en fin
Août ;
· faire des prévisions de récoltes
céréalières courant le mois de septembre de chaque
année afin de tenir informés le gouvernement et ses partenaires
au développement sur la situation de la campagne agricole. Ces
prévisions permettent d'établir un bilan céréalier
prévisionnel ;
· faire des estimations des stocks résiduels
paysans courant septembre ;
· suivre l'évolution du paradigme
sécurité alimentaire ;
· servir à l'évaluation des performances
du secteur agricole. Ces estimations sont utilisées pour
l'établissement du bilan céréalier.
L'approche retenue pour la mise en oeuvre de l'EPA (2015/2016)
est un sondage à deux degrés avec stratification induite au
premier degré par celle du deuxième degré. L'unité
primaire est le village tel que retenu par le Recensement Général
de la Population et de l'Habitat de 2006. Le tirage des unités primaires
est fait à probabilité proportionnelle à la taille en
ménages agricoles. Les unités secondaires sont tirées par
la méthode du sondage aléatoire simple (Révision
SAWADOGO Israel-- ISE 3-- ENSAE
MARAHASA/DPPO-BF
20
Barrières et opportunités à
l'adoption des techniques de CES/DRS au Burkina Faso, dans la zone
sahélienne
méthodologique de l'Enquête Permanente Agricole,
MARHASA). Voir Annexe A (A.1) pour la méthode de pondération et
la forme des estimateurs.
Zone d'étude
Le champ de cette étude constitue la zone
sahélienne burkinabè. Elle est située au Nord du pays
entre les latitudes 13°C'5' N et 15°C'3' N. Sur le plan climatique,
elle est caractérisée par une pluviométrie de moins de 600
mm, des températures extrêmes allant de 10 à 45°C et
une saison pluvieuse de 2 à 3 mois. La végétation dans
cette zone est essentiellement dominée par les arbustes épineux,
les steppes arbustives et les dunes de sable rencontrées plus au nord.
Trois régions composent principalement cette zone : la région du
Nord, le Sahel et la région du Centre Nord.
Graphique 1: carte climatique du Burkina
Faso
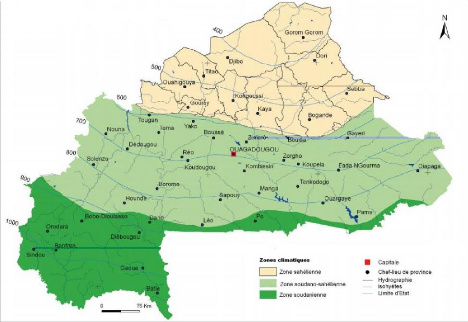
Source : Centre de recherche forestière
international (CIFOR)
Le choix de cette zone se justifie par les
caractéristiques climatiques défavorables qu'elle
présente, des caractéristiques qui rendent l'agriculture dans
cette zone vulnérable au phénomène d'érosion, de
sécheresse, de désertification, etc. C'est donc une zone dans
laquelle l'utilisation des techniques
SAWADOGO Israel-- ISE 3-- ENSAE
MARAHASA/DPPO-BF
21
Barrières et opportunités à
l'adoption des techniques de CES/DRS au Burkina Faso, dans la zone
sahélienne
CES/DRS est justifiée. Cette situation rend
l'étude de l'adoption des techniques antiérosives plus pertinente
dans la zone sahélienne.
Détermination des barrières à
l'adoption des techniques CES/DRS
Le premier axe de notre étude est la
détermination des barrières à l'adoption des techniques de
CES/DRS au Burkina Faso, précisément dans la zone
sahélienne. Pour faire ressortir ces barrières, il serait
nécessaire d'analyser l'adoption de ces techniques de la part des
agriculteurs. Cette analyse se fera en déterminant l'influence qu'ont
les différents facteurs sur la probabilité que les techniques de
CES/DRS soient adoptées sur une exploitation agricole donnée. Par
la suite, les facteurs ayant une influence négative seront
considérés comme les barrières à l'adoption des
techniques de conservation et de défense des eaux et sols. Compte tenu
de l'aspect dichotomique du phénomène étudié et des
informations recueillies dans la littérature, les modèles
adéquats pour nos données seront les modèles
dichotomiques3. De plus, ces modèles donnent la
possibilité de déterminer à quel degré varie la
probabilité d'adoption en fonction de plusieurs facteurs explicatifs de
façon synthétique, contrairement à une simple analyse
descriptive. L'utilisation des modèles dichotomiques est
récurrente dans les études sur les déterminants de
l'adoption des techniques agricoles. On distingue en guise d'exemples
l'étude menée par Baradi (2005) sur l'adoption du labour de la
terre, celle menée par Bayard et al. (2006) sur l'adoption des cordons
pierreux à Fort-Jacques (Haïti) ; les travaux menés par
Ng'ombe (2014) sur le comportement d'adoption des pratiques de conservation au
niveau des ménages agricoles zambiens, etc. La confrontation des
méthodes utilisées dans la littérature à la
structure des données dont nous disposons nous conduit à opter
pour l'utilisation d'un modèle économétrique dichotomique
dans le but de déterminer les barrières liées à
l'adoption de la CES/DRS. De ce fait, il serait nécessaire de
décrire le cadre théorique de ces modèles.
Présentation du modèle
dichotomique
La seconde moitié du XXème
siècle fut dominée par l'utilisation des données
microéconomiques dans le but d'expliquer le comportement des agents
économiques. L'étude de tels comportements a rendu
nécessaire le développement de modèles
économétriques permettant d'étudier les
3 La variable d'intérêt qui est
l'adoption des CES/DRS présente une structure dichotomique. La
décision d'adoption de chaque agriculteur est renseignée sans
aucune précision du type de technique utilisé.
SAWADOGO Israel-- ISE 3-- ENSAE
MARAHASA/DPPO-BF
22
Barrières et opportunités à
l'adoption des techniques de CES/DRS au Burkina Faso, dans la zone
sahélienne
phénomènes décrits par des variables de
nature qualitative. Globalement, 3 types de modèle ont été
développés dans ce cadre. Il s'agit des modèles
dichotomiques, des modèles polytomiques et des modèles
appliqués aux données censurées ou tronquées.
Les modèles dichotomiques (logit et probit) ont
initialement été utilisés dans le domaine de la biologie,
de la sociologie et de la psychologie avant d'atteindre l'économie avec
principalement les travaux de MacFadden (1974) et Heckman (1976).
De façon générale, ces modèles
sont utilisés dans le but de déterminer l'influence de certains
facteurs (variables explicatives) sur un phénomène H
pouvant être décrit par une variable dichotomique y
donnée. Le phénomène d'intérêt dans
notre cas est l'adoption des techniques de CES/DRS. En notant N la taille de
l'échantillon d'exploitations agricoles dont nous disposons, y
la variable dichotomique associée à l'adoption des
techniques peut être décrite comme suit :
1, si au moins une technique de CESIDRS
V i = 1 ...N, on a: est adoptée par l'individu i
(1)
yi =
0, sinon
De façon analytique, le modèle dichotomique sera
construit dans le but d'expliquer, à partir des observations des
variables explicatives faites sur chaque individu i notées
xi, la probabilité que le phénomène «
adoption » se réalise au niveau de cet individu. Cette
probabilité est notée pi = Prob(y1 = 11x1). Les p
variables explicatives utilisées sont réparties en trois
groupes: les caractéristiques économiques du responsable de
l'exploitation, ses caractéristiques sociodémographiques et les
caractéristiques de la surface emblavée. Par ailleurs, la
description de la variable y fait intervenir une variable latente
y* qui s'écrit comme combinaison linéaire des
variables explicatives : y* = xil3 + e , avec x le
vecteur des variables explicatives et il3 celui
des coefficients associées.
Ainsi l'expression (1) peut se réécrire comme suit
:
|
V i= 1 ...N, on a: y1=
|
f1, si yti* > c
l 0, sinon avec c un seuil réel
fixé4
|
4 Réel à parti duquel l'on
prédira la réalisation du phénomène
d'intérêt
SAWADOGO Israel-- ISE 3-- ENSAE
MARAHASA/DPPO-BF
23
Barrières et opportunités à
l'adoption des techniques de CES/DRS au Burkina Faso, dans la zone
sahélienne
L'effet des variables explicatives sur la variable
d'intérêt peut être cerné par le canal de la variable
latente Y, . La probabilité pi est
déterminée de la manière suivante:
pi = Prob(Yi = 11xi) = Prob(Yi * >_ c) = Prob(xif3 + E
>_ c)
=> pi=??(xif3- c)
Où i/.' désigne la fonction de
répartition de la loi associée au terme d'erreur E. On
parlera de modèle logit lorsque cette loi est logistique et de
modèle probit lorsqu'elle est normale.
Choix entre le modèle probit et
logit
Les modèles logit et probit présentent une
ressemblance au niveau des coefficients estimés mais ils ne
réagissent pas de la même façon face aux valeurs
extrêmes. Ces valeurs ont en réalité un poids plus
important avec un modèle logit qu'avec un modèle probit.
Cependant, dans le cadre de cette étude sera utilisé le test de
Hausman pour vérifier la significativité de la différence
entre les coefficients estimées avec un modèle probit et ceux
estimés avec un modèle logit. A l'issu des résultats de ce
test nous déterminerons le modèle à retenir pour la suite
de l'analyse.
Méthode d'estimation
La méthode d'estimation utilisée est celle du
maximum de vraisemblance. Le choix de cette méthode est dû aux
différents problèmes liés à l'estimation des
paramètres d'un modèle dichotomique par les moindres
carrés ordinaires (voir Annexe A, A.2). Le phénomène
d'adoption tel que décrit par le modèle (1) suit une loi
binomiale avec une probabilité de réalisation de pi pour
chaque exploitation i. Le logarithme de la vraisemblance est donc
donnée par :
N
ln L(Y, x, f3) = I Yi ln(i (xif3)) + (1 - Yi) ln(1 -
1(xif3))
i=1
Les coefficients du vecteur f3 sont
déterminés en résolvant les équations
résultant de l'annulation des dérivées partielles
premières de cette log-vraisemblance sous les conditions de second
ordre. Cette étape est suivie des travaux de validation du
modèle. Il s'agit de vérifier, après une analyse des
résidus, la significativité globale des coefficients
estimés, la qualité de la prédiction du modèle et
son adéquation aux données.
SAWADOGO Israel-- ISE 3-- ENSAE
MARAHASA/DPPO-BF
24
Barrières et opportunités à
l'adoption des techniques de CES/DRS au Burkina Faso, dans la zone
sahélienne
Validation du modèle dichotomique
Méthode d'analyse des résidus
Il s'agira à cette étape de faire une analyse
visant à identifier les individus ayant des comportements
irréguliers à travers le modèle dichotomique. Nous
utiliserons les 4 principaux outils rencontrés dans la
littérature:
? Les résidus standardisés de Pearson, pour
déterminer les outliers, comparés à 2,
? Le "laverage", permettant de détecter les "high
laverages", comparé à 2(p + 1)/N
? La distance de Cook pour mesurer l'influence de chaque
individu sur les coefficients estimés, elle est comparée à
4/N ;
? Le dbeta pour déterminer l'influence de chaque
individu aussi bien sur la valeur des coefficients estimés que sur leur
signe, il est comparé à 2/vN ;
L'utilisation de ces 4 outils permettra d'identifier, comme
individus pouvant détériorer la qualité du modèle,
les individus qui apparaissent irréguliers pour plus de deux
distances.
Le test du rapport de maximum de vraisemblance (LR
Test)
Les coefficients estimés permettront de
déterminer l'influence de certains facteurs sur le comportement
d'adoption des techniques CES/DRS. Cependant, pour un facteur donné,
cette influence est-elle significative dans le modèle? C'est pour
répondre à cette question que sera utilisé dans cette
étude le test de significativité globale ou partielle par le
rapport de maximum de vraisemblance (LR test). En effet, le LR test peut
être utilisé pour vérifier la significativité d'un
ou de plusieurs coefficients en comparant les valeurs de vraisemblance
atteintes pour le modèle contraint et celui non contraint. Le
déroulement du LR test est présenté en annexe (annexe A,
A.3). La vérification de la significativité partielle ou globale
des coefficients sera suivie d'un contrôle de qualité du
modèle en termes de pouvoir prédictif.
La matrice de confusion
La capacité du modèle dichotomique à
prédire l'adoption des techniques de CES/DRS est donnée par la
matrice de confusion. Fondamentalement, c'est une matrice qui fournit les
différents types de classification et le pourcentage associé
à chaque type. Les types de classification désignent les bonnes
et mauvaises prédictions et les pourcentages associés
désignent respectivement les taux de
SAWADOGO Israel-- ISE 3-- ENSAE
MARAHASA/DPPO-BF
25
Barrières et opportunités à
l'adoption des techniques de CES/DRS au Burkina Faso, dans la zone
sahélienne
bonnes et de mauvaises prédictions. Le taux de bonnes
prédictions est la proportion des exploitations agricoles de
l'échantillon dont la classe prédite correspond exactement
à la classe dans laquelle elle se trouve tandis que le taux de mauvaises
prédictions est la proportion des exploitations mal classées.
Dans le cas de l'étude de l'adoption des CES/DRS la matrice de confusion
se présentera comme suit :
Tableau 1: matrice de confusion
théorique
Adoptantes Non adoptantes
(observation) (observation)
Adoptantes A B
(prédiction)
Non adoptantes C D
(prédiction)
Source : construction de
l'auteur
Avec N la taille de l'échantillon, le taux de bonnes
prédictions vaut A+??
?? .
La sensibilité et la spécificité du
modèle sont déduites de cette matrice. La sensibilité ici
représentera la probabilité de bien classer une unité de
production agricole de la catégorie des adoptantes tandis que la
spécificité désignera la probabilité de bien
classer une unité de la classe
inverse. Lorsqu'on se réfère au tableau 1, la
spécificité est donnée par la quantité
??
??+?? et la
sensibilité par A
A+?? .
Ces indicateurs apportent des informations sur le pouvoir
prédictif du modèle lorsqu'on considère un seuil
donné de probabilité au-delà duquel l'on peut
prédire l'adoption des techniques de CES/DRS. Par ailleurs, avec la
courbe ROC, nous déterminerons les couples de niveaux de
sensibilité et de spécificité atteints pour tout seuil
d'adoption5.
La courbe ROC
La courbe ROC est une méthode de représentation
graphique des performances d'un discriminant en deux classes. Elle permettra
dans cette étude de mettre en relation la sensibilité et la
spécificité du modèle discriminant (logit ou probit) en
fonction des seuils d'adoption. En effet pour tout seuil, il est reporté
sur l'axe des abscisses la valeur de la spécificité du
modèle et sur l'axe des ordonnées la valeur de la
sensibilité atteinte. L'ensemble des couples de coordonnées forme
ainsi la courbe
5 Seuil auquel on compare les probabilités
prédites pour prédire si l'individu est un adoptant ou un non
adoptant.
SAWADOGO Israel-- ISE 3-- ENSAE
MARAHASA/DPPO-BF
26
Barrières et opportunités à
l'adoption des techniques de CES/DRS au Burkina Faso, dans la zone
sahélienne
ROC. L'aire située en dessous de la courbe ROC, variant
entre 0,5 et 1, est un indicateur de la qualité de la classification
faite par le modèle. Le pouvoir discriminant du modèle sera
d'autant plus grand que le sera cette aire.
Tests de bonne spécification de Pearson et de
hosmer-lemeshow
Les tests de Hosmer-Lemeshow et Pearson seront utilisés
dans cette étude pour évaluer la performance du modèle
dichotomique décrivant l'adoption des techniques de CES/DRS en termes
d'ajustement aux données. De façon concrète, ce test
vérifie la significativité de l'écart entre les
fréquences prédites et les fréquences observées de
la variable d'intérêt. L'hypothèse nulle du test est que
« le modèle s'ajuste bien aux données » et il se fait
en 3 étapes :
? Etape 1 : l'on regroupe les probabilités
prédites selon une répartition donnée en classes. On
obtient à cette étape les fréquences prédites pour
la variable d'intérêt.
? Etape 2 : les fréquences de bonnes réponses et
celles de mauvaises réponses sont aussi déterminées pour
chacune des classes construites à l'étape 1. Les
fréquences obtenues désigneront donc les fréquences
observées.
? Etape 3 : l'on évalue la distance entre les
fréquences prédites et celles observées.
L'hypothèse nulle est acceptée lorsque la
distance évaluée entre les fréquences prédites et
observées est statistiquement faible. Dans les cas d'un test de Pearson,
les classes sont composées des individus qui ont une même
probabilité prédite. Dans le cas d'un test de Hosmer-Lemeshow, le
découpage en classe est fait par rapport aux quantiles. Les statistiques
et les règles de décision de ces deux tests sont données
en annexe (Annexe A, A.4).
Variables utilisées dans la détermination
des barrières à l'adoption
Dans les travaux empiriques sur les déterminants de
l'adoption des techniques CES/DRS, les types de variables récurrents
sont les variables sociodémographiques (Featherstone et Goodwin ,1993;
Gould et al, 1989; Norris and Batie, 1987), organisationnelles (Francis 1986)
et économiques (Baidu-Forso, 1999) et les caractéristiques de la
surface cultivée (Rahm et Huffman, 1984 ; Barbier 1990 ; Lee et Stewart,
1983). Ces différentes références justifient le choix des
trois types de variables explicatives pour l'estimation du modèle
dichotomique de la détermination des barrières à
l'adoption des techniques de CES/DRS.
SAWADOGO Israel-- ISE 3-- ENSAE
MARAHASA/DPPO-BF
27
Barrières et opportunités à
l'adoption des techniques de CES/DRS au Burkina Faso, dans la zone
sahélienne
Tableau 2: Variables expliquant l'adoption des
CES/DRS et effets attendus
|
Groupe de variables
|
Variable
|
Effet attendu
|
|
Caractéristiques
Sociodémographiques
|
Sexe (référence femme) Age
Taille ménage
|
+
+
+
|
|
Niveau d'instruction (référence=non
alphabétisé)
Alphabétisé autre langue
Alphabétisé en français
|
+
+
|
|
Ne pas être chef de ménage Non adhésion
à OP
|
-
-
|
|
Caractéristiques de
l'exploitation
agricole
|
Superficie labourée Labour attelé
Labour motorisé Labour manuel
|
-
-
-
|
|
Superficie sécurisée par
Sécurisation moderne Sécurisation traditionnelle
|
+
+
|
|
Relief du champ
Superficie sur plateau
Superficie dans basfond
|
Ambiguë
-
|
|
Type de gestion Collective
|
+
|
|
Caractéristiques
économiques de
l'exploitation
et du responsable
|
Autres activités
Main oeuvre rémunérée Cheptel petits
animaux
Cheptel grands animaux
|
-
-
+
+
|
Source : Construction de l'auteur, revue
empirique des déterminants de l'adoption
Les variables sociodémographiques prises en compte dans
le cadre de cette étude seront l'âge, le sexe, la taille du
ménage du responsable de l'exploitation, le niveau d'instruction et le
fait que le responsable soit un chef de ménage ou pas. Le niveau
d'instruction est décrit par trois modalités : non
alphabétisé, alphabétisé en langue française
et alphabétisé en d'autres langues différentes du
français.
Les modalités de gestion et autres
caractéristiques de la surface exploitée sont décrites par
les types de labour, le type de gestion, le relief de la parcelle et son niveau
de sécurisation. Les types de labour sont donnés par les parts de
surface labourées par attelage, par motorisation ou par des outils
manuels. Le type de gestion est aussi exprimé en termes de proportion du
champ gérée de façon collective. Le relief est
déterminé par les proportions de la superficie situées sur
un plateau et dans
SAWADOGO Israel-- ISE 3-- ENSAE
MARAHASA/DPPO-BF
28
Barrières et opportunités à
l'adoption des techniques de CES/DRS au Burkina Faso, dans la zone
sahélienne
un bas-fond. Le niveau de sécurisation de la terre est
aussi décrit par les parts de la superficie sous sécurisation
foncière traditionnelle, sous sécurisation foncière
moderne et sous aucune sécurisation foncière.
L'aspect économique de l'exploitation agricole est
prise en compte à travers, le nombre d'animaux de petite taille
(caprins, ovins et porcins), le nombre d'animaux de grande taille (bovins,
équins et camelins) possédés, l'utilisation d'une main
d'oeuvre rémunérée (1 en cas d'utilisation, 0 dans le cas
contraire) et le recours à d'autres activités (1 si l'exploitant
exerce une activité non agricole, 0 sinon).
La détermination des barrières à
l'adoption des techniques de conservation et de défense des eaux et sols
contribuera à mettre en exergue les facteurs sur lesquels l'on doit
s'appuyer pour promouvoir leur utilisation. A ce niveau il est important que
l'agriculteur, étant confronté à un choix, connaisse a
priori les avantages liés à l'adoption de ces techniques,
avantages que nous déterminerons à l'aide d'une frontière
de production.
Construction de la frontière de
production
L'analyse des opportunités d'adoption des CES/DRS
constitue le second axe de cette étude. Elle se fera en deux
étapes : la construction de la frontière de production et la
détermination des effets de certaines variables sur
l'inefficacité technique y compris l'adoption de l'utilisation des sites
antiérosifs. Cette analyse sera faite sur les cultures qui couvrent la
plus grande partie de la superficie totale emblavée dans la zone
d'étude. Pour chaque culture, une frontière de production
à l'hectare (rendement) est estimée afin de déterminer
l'effet de l'adoption de la CES/DRS sur le degré d'inefficacité
technique des exploitations agricoles. Ce procédé s'explique par
le fait que le rendement soit lié à l'espèce
végétale cultivée. A titre d'exemple, il serait
impertinent d'analyser dans un même modèle le rendement d'une
exploitation de coton et le rendement d'une parcelle de chou du fait de leur
différence en poids et en surface nécessaire pour le
développement des plantes. Ce procédé n'est pas nouveau,
il est retrouvé dans plusieurs travaux empiriques sur les
déterminants de l'efficacité technique. C'est le cas des travaux
de Shively (1998) basés sur la culture du maïs, ceux de Baten et al
(2009) basés sur la culture du thé et ceux de Fontan (2008)
basés sur la culture pratiquée en majorité sur les
superficies irriguées, le riz.
SAWADOGO Israel-- ISE 3-- ENSAE
MARAHASA/DPPO-BF
29
Barrières et opportunités à
l'adoption des techniques de CES/DRS au Burkina Faso, dans la zone
sahélienne
Dans la littérature économétrique, deux
familles de méthodes de construction des frontières de production
sont proposées. On distingue les méthodes paramétriques et
les méthodes non paramétriques. Au niveau des méthodes
paramétriques nous distinguons les frontières de production
déterministes et les frontières de production stochastiques.
Frontière de production
déterministe
Les frontières de production déterministes,
développées par Aigner et Chu (1968) décrivent la
quantité produite, en fonction de la quantité potentielle,
à un terme d'erreur près qui détermine
l'inefficacité du système de production. La production maximale
est déterminée par les quantités données d'input et
les paramètres à estimer. De façon analytique, le
modèle général s'écrit comme suit :
V i = 1, ... , N on a yl = q (xl, [3) - ul , ul
>_ 0 (1)
Avec yl la production observée chez le
producteur i , [3 le vecteur des paramètres
associés au vecteur xl representant les quantités
d'inputs qu'il a utilisé et ul l'écart entre la
production observée et la production maximale q (xl, [3)
(frontière). Le terme ul est déterminé
uniquement par l'inefficacité technique du système de production:
c'est pourquoi la frontière est dite ici déterministe.
Le vecteur de paramètre [3 peut être
estimé par des méthodes statistiques ou non statistiques. En ce
qui concerne les méthodes non statistiques, les paramètres sont
obtenus en résolvant un problème de minimisation des
résidus unilatéraux sous la contrainte ul >_ 0 qui
est équivalent à yl <_ q (xl, [3) , V i = 1, ... , N.
L'on a recours à la programmation linéaire (min E |yl - q
(xl,[3)|) ou quadratique (min E |yl - q (xl, [3)|2 )
pour estimer les paramètres de la frontière de production. Ces
méthodes ont été développées par Aigner et
Chu (1968). Cependant, les paramètres estimés de la sorte sont
dépourvus de propriétés statistiques en plus de leur
extrême sensibilité aux valeurs extrêmes. Pour pallier
à ces problèmes, des méthodes statistiques ont
été développées par Richmond (1974).
Trois principales méthodes statistiques sont
proposées : la méthode des moindres carrés corrigés
; la méthode des moindres carrés décalés et la
méthode du maximum de vraisemblance. Sans perte de
généralité, (1) peut être réécrit pour
l'individu i sous la forme:
SAWADOGO Israel-- ISE 3-- ENSAE
MARAHASA/DPPO-BF
30
Barrières et opportunités à
l'adoption des techniques de CES/DRS au Burkina Faso, dans la zone
sahélienne
???? = ??0 + ? ?? ?????????? - ???? , ???? = 0 (2)
La première méthode d'estimation est
basée sur les hypothèses de l'identique distribution des termes
d'erreurs et de la non corrélation de ces termes aux inputs. Sous ces
hypothèses, les
|
^
paramètres estimés sont sans biais à
l'exception de la constante ??0
|
(En effet ??(??0^
|
) = ??0 + ?? ) .
|
Pour corriger ce défaut, Richmond (1974) intègre
un terme supplémentaire à l'équation (2) comme suit : ????
= ??0 + ? ?? ?????????? - ?? , avec ?? = -???? + ?? . Ainsi, par la
méthode des moindre carrées
^
ordinaires, on estime les paramètres ???? sans biais
pour tout j et en retranchant la moyenne du terme u à
la constante obtenue on obtient des estimateurs étant tous sans biais.
Cependant l'application de cette méthode peut aboutir à des
résidus négatifs ce qui signifie qu'il y a possibilité que
certains individus soient situés au-delà de la frontière.
Une telle frontière n'obéit pas rigoureusement à la
logique d'une frontière de production déterministe (voir la
contrainte dans le modèle (2)). C'est ce problème que cherchera
à résoudre Greene (1980) en appliquant une translation sur le
terme á, ???? ' = ?????? ???? - ????, afin d'obtenir des termes
d'erreur étant tous positifs. C'est en cela que consiste la
méthode des moindres carrés décalés. Cette
méthode respecte la contrainte de positivité des résidus
même si elle ne permet pas de déterminer la distribution
asymptotique du terme constant.
Sous les hypothèses de l'identique distribution des
termes d'erreurs et de la non corrélation de ces termes aux inputs, en
spécifiant une loi pour le terme u, la méthode de
maximum de vraisemblance peut être utilisée pour estimer les
valeurs des paramètres de la frontière. Lorsque cette loi est
asymétrique l'on obtient des résultats meilleurs que ceux obtenus
par les moindres carrés ordinaires (Greene, 1980).
Quelle que soit la méthode d'estimation des
frontières déterministes, leur analyse est limitée par le
fait qu'elles n'intègrent pas les facteurs extrinsèques au
système de production dans la détermination de
l'inefficacité/efficacité économique. Pourtant certains
secteurs de production comme l'agriculture sont beaucoup sensibles aux facteurs
environnementaux, des facteurs qui ne peuvent pourtant pas être
complètement maitrisés par le producteur. Les modèles de
frontière de production déterministe ne sont donc pas conformes
aux données dont nous disposons car, étant du domaine agricole,
elles sont beaucoup influencées par les facteurs climatiques. Les
limites observées au niveau de l'analyse par frontière de
production déterministe ont donné lieu au
SAWADOGO Israel-- ISE 3-- ENSAE
MARAHASA/DPPO-BF
31
Barrières et opportunités à
l'adoption des techniques de CES/DRS au Burkina Faso, dans la zone
sahélienne
développement de la notion de frontière de
production stochastique. Cette dernière notion est celle qui sera
utilisée dans le cadre de cette étude pour déterminer le
lien entre adoption des techniques de CES/DRS et l'efficacité
technique.
Construction de la frontière de production
stochastique
Les concepteurs de ce modèle sont Aigner, Lovell et
Schmidt (1977) ; Meusen et Van Den Broeck (1977) et il se présente comme
suit :
V i = 1, ... , N on a : yl = q (xl, )l3) - ul + vl avec
ul >_ 0 et vl E R
Ou yl = q (xl,)l3) + el en posant el = -ul +
vl
Dans ce modèle, l'écart observé entre la
production obtenue et la frontière de production admet deux composantes.
La première, ul, est due au fonctionnement du système de
production et la seconde, vl, est stochastique et prend en compte tous
les facteurs extrinsèques susceptibles d'influencer la performance du
processus de production tels que les facteurs climatiques (Aigner, Lovell et
Schmidt 1977 ) . La frontière de production est dite stochastique
à cause de cette dernière composante. La frontière de
production stochastique est donnée par q(xl,)l3) +
vl. Ainsi, toute déviation de cette frontière est due au
fonctionnement de la firme, c'est-à-dire son inefficacité
technique.
La frontière de production est estimée en ayant
recours à la méthode du maximum de vraisemblance. Une
méthode dite des moindres carrés modifiés est aussi
utilisée pour estimer la frontière de production, mais cette
méthode conduit à des estimateurs qui ne sont ni consistants ni
efficaces car, contrairement aux estimateurs issus de la méthode du
maximum de vraisemblance, ils n'atteignent pas la borne de Cramer-Rao (Parmeter
et Kumbhakar, 2014).
III.3.1 Estimation: méthode du maximum de
vraisemblance
L'utilisation de la méthode du maximum de vraisemblance
nécessite des hypothèses distributionnelles émises sur les
termes composant l'erreur. Plusieurs distributions sont utilisées dans
les différents développements faits sur l'analyse par
frontière de production stochastique. Initialement, on distingue la loi
normale et la loi semi normale utilisée par However, Aigner et al.
(1977) pour décrire l'évolution respective du terme
d'inefficacité technique u et du terme stochastique v.
En gardant l'hypothèse faite sur la distribution du terme v,
Stevenson (1980)
SAWADOGO Israel-- ISE 3-- ENSAE
MARAHASA/DPPO-BF
32
Barrières et opportunités à
l'adoption des techniques de CES/DRS au Burkina Faso, dans la zone
sahélienne
considère que le terme d'inefficacité est
distribué selon une loi normale tronquée. Les modèles
basés sur ces deux considérations distributionnelles sont les
plus usités dans les travaux empiriques (Parmeter et Kumbhakar, 2014),
mais deux autres types de distribution apparaissent dans la littérature
économétrique.
Dans certains modèles spécifiques la
distribution utilisée pour décrire l'évolution de
l'inefficacité technique est la loi normale tandis que d'autres
modèles considèrent plutôt la loi gamma ou exponentielle.
Par ailleurs, le choix de la distribution adéquate dans l'estimation
d'une frontière de production stochastique est une étape
importante car les estimations obtenues sur les niveaux d'inefficacité
des individus en dépendent considérablement. Le problème
majeur est qu'il n'existe pas de méthode spécifique permettant de
déterminer la meilleure distribution adéquate à
l'estimation de la frontière de production (Parmeter et Kumbhakar,
2014). Dans le cadre de cette étude, nous estimerons la frontière
de production en considérant la distribution normale pour le terme
stochastique et les distributions semi normale ou normale tronquée pour
le terme d'inefficacité technique. Il faudra noter que la loi semi
normale est une loi normale tronquée à moyenne nulle. Ainsi, pour
déterminer laquelle des deux spécifications serait adaptée
aux données, nous testerons la nullité de la moyenne de la
distribution tronquée en estimant une frontière de production
avec un terme d'inefficacité suivant une loi normale tronquée.
En supposant que le terme d'inefficacité et le terme
stochastique suivent respectivement la loi normale ??(0, ????2 ) et
une loi normale tronquée ???? +(??, ????2) ,
à partir de la densité jointe de u et v
|
on obtient la densité marginale de ?? : ?????? +(??)
=
|
?? ??(??+??
1 ?? )??( ?? ? ??? -????? ? )
??( ?? ????) . Lorsqu'on suppose une
|
distribution semi normale pour le terme d'inefficacité
technique, la densité de ?? est donnée par :
????+(??)=2 ?? ??(??? ?)??(- ????? ? ) , Avec
??2=????2 +????2 et
=????/???? .
Ce modèle considère que les termes d'erreurs sont
homoscédastiques,
Le paramètre ?? s'interprète comme la
variabilité relative des sources de déviation par rapport
à la production maximale devant être atteinte. Il permet de
déterminer la source qui détermine le plus cette
déviation. Cependant l'interprétation de ce paramètre doit
se faire avec beaucoup de précautions. En effet dans le cas où le
terme d'inefficacité technique est supposé suivre une loi
SAWADOGO Israel-- ISE 3-- ENSAE
MARAHASA/DPPO-BF
33
Barrières et opportunités à
l'adoption des techniques de CES/DRS au Burkina Faso, dans la zone
sahélienne
semi normale ou normale tronquée, sa variance est
donnée par (1 - 2??) ????2 en lieu et place de
????2 . Ainsi la part des déviations des productions
observées par rapport à la frontière due à
l'inefficacité
2
technique est évaluée à ??=
(1-2 ??)???? (1-2 ??)???? 2+????2 .
?? et ?? désignent respectivement les fonctions de
répartition et de densité de la loi normale centrée
réduite.
Les logarithmes des vraisemblances s'écrivent
respectivement comme suit :
|
????
|
L????
|
=
|
-?? ????
???? L??+
|
??
?(????
??-
|
2
+ ??)
|
-
????
|
??
??
|
????
|
??
??=1
1
|
|
-
|
???? ? ?)
|
|
??=1
= -?? ???? ??
|
??
??
+ ?
??=1
|
??(????)
??
(-????
|
????
( ??
??
?????2
??=1
|
??
|
|
??)
|
2??2
|
En annulant les dérivées premières de la
fonction de vraisemblance, on obtient une estimation des paramètres ?? ,
?? ???? ??2 par le maximum de vraisemblance. Cependant le principal
but de l'estimation de la frontière de production consiste à
déterminer l'effet de l'adoption des techniques CES/DRS sur le niveau
d'efficacité technique des agriculteurs.
Test d'hypothèses sur les termes
d'erreur
Avant de procéder à une modélisation de
l'efficacité technique, il convient de s'assurer que l'estimation d'une
frontière de production en lieu et place d'une fonction de production
issue d'une régression linéaire est justifiée.
L'hypothèse de l'existence d'un terme d'inefficacité technique
constitue donc la première hypothèse fondamentale de l'estimation
d'une frontière de production. Le rejet de cette hypothèse
impliquera la non nécessité de recourir à l'estimation
d'une frontière de production, une fonction de production
moyenne6 serait donc adaptée aux données. Le test de
détection de la présence d'un terme d'efficacité technique
utilisé dans le cadre de cette étude est le z-test
développé par Coelli (1995). Selon Coelli (1995), en
présence d'un terme d'efficacité technique, la distribution des
résidus issus d'une régression par les moindres carrés
ordinaires est
6 Les méthodes d'estimation des fonctions de
production par les moindres carrés estiment une fonction de production
moyenne et ne tiennent pas compte de la notion de maximalité
associé à l'analyse par les frontières de production.
SAWADOGO Israel-- ISE 3-- ENSAE
MARAHASA/DPPO-BF
34
Barrières et opportunités à
l'adoption des techniques de CES/DRS au Burkina Faso, dans la zone
sahélienne
négativement asymétrique. A partir de cette
assertion et de l'hypothèse nulle d'absence de terme
d'inefficacité technique, il construit une statistique (z-statistique)
du test à base des moments
d'ordre 2 (??2) et 3 (??3) de ces
résidus. La z-statistique est donnée par : z = ??3
.
(6??2 3
?? )
La seconde considération à vérifier est
la présence d'un facteur aléatoire dans le processus de
production des agriculteurs. Cela revient à tester la nullité de
la variance du terme stochastique a??2. L'application d'un
test classique de rapport de maximum de vraisemblance permet de vérifier
l'existence d'un effet stochastique dans la détermination de la
production potentielle des agriculteurs.
La vérification de ces considérations permet
d'atteindre l'objectif principal de l'estimation d'une frontière
stochastique, dans cette étude, qu'est l'appréciation de l'effet
de l'adoption des CES/DRS sur le terme d'efficacité technique.
III.3.2 Méthode d'appréciation de
l'effet de l'adoption des techniques de CES/DRS sur l'inefficacité
technique
La détermination de l'effet qu'ont d'autres variables
sur le niveau d'efficacité peut se faire en deux étapes ou en une
seule étape. Procéder en deux étapes consiste à
déterminer en une première étape les scores
d'inefficacité sans tenir compte des variables expliquant ce score et en
une seconde étape procéder à une régression sur le
score pour déterminer l'impact de ces variables sur
l'inefficacité. Cette méthode est pourtant
déconseillée par plusieurs auteurs du domaine de l'estimation des
frontières stochastiques tels que Kumbhakar et Lovell (2000), Wang et
Schmidt (2002). En effet l'estimation faite au niveau de la première
étape ignore la probable existence d'une
hétéroscédasticité au niveau des termes d'erreur.
En cas d'hétéroscédasticité du terme v,
les paramètres de la frontière de production estimés sont
consistants exceptée la constante qui est biaisée et le biais
obtenu sur ce paramètre se propage sur les scores d'inefficacité
estimés à la seconde étape. Au niveau du terme
d'inefficacité technique, la présence d'une
hétéroscédasticité biaise les paramètres de
la frontière et donc les scores d'inefficacité estimés
(Kumbhakar et Lovell, 2000). L'alternative à ces problèmes est
l'estimation de la frontière de production et de l'influence de
certaines variables exogènes sur l'inefficacité ou sur le bruit
en une seule étape (Kumbhakar et Lovell, 2000). Pour déterminer
l'effet de l'adoption des techniques de CES/DRS sur le niveau
d'efficacité des agriculteurs, nous supposerons une
hétéroscédasticité sur le terme
d'inefficacité.
SAWADOGO Israel-- ISE 3-- ENSAE
MARAHASA/DPPO-BF
35
Barrières et opportunités à
l'adoption des techniques de CES/DRS au Burkina Faso, dans la zone
sahélienne
Dans le domaine agricole le principal aspect pouvant
influencer la variance du terme stochastique est la taille de l'exploitation.
Cette éventuelle influence pourrait être neutralisée par le
fait que l'analyse soit basée sur des quantités obtenues (output)
ou consommées (inputs) par unité de surface (ha).
La prise en compte de
l'hétéroscédasticité du terme d'inefficacité
permet de déterminer l'effet de l'adoption des techniques de CES/DRS sur
l'inefficacité technique.
Cas où le terme d'inefficacité suit une
loi semi-normale : hypothèse de la nullité ??
acceptée
La prise en compte de
l'hétéroscédasticité des variances des
différents termes d'erreur se fait par l'adoption des
paramétrisations suivantes:
2 = ????,?? ????
, ? ??= 1, ... ,??
???? ???2 ?,?? = ????,?? ????
Avec ???? le vecteur des variables expliquant la variance du
terme d'inefficacité technique et ???? le vecteur des coefficients
associés à ces variables; ???? le vecteur des variables
expliquant la variance du terme stochastique et ???? le vecteur des
coefficients associés à ces variables.
Dans ce cas, le logarithme de la vraisemblance ???? L??+
s'écrira sous la forme:
?? ?? ??
2
+ ?log (1 - ?? (???? ???? 2 ? ????
???? L??+ = -????? ????
??=1
1
2 )) - 2
???? ????
??=1 ??=1
La résolution du programme de minimisation donne les
paramètres associés aux intrants et aux facteurs expliquant le
niveau d'inefficacité. Particulièrement, le signe d'un
coefficient ???? , ?? allant de 1à K (nombre de variables explicatives),
détermine le sens de l'impact de la variable explicative associée
sur le niveau d'efficacité technique mais ne peut en aucun cas
être considéré comme un effet marginal. En effet, Suite
à l'estimation à l'aide de la distribution semi normale, le
niveau d'inefficacité de l'exploitation i prédit est
donné par : ??(????) = v2/?? . ??????,?? ????.
Les effets marginaux des variables expliquant
l'inefficacité technique sont individuels mais l'on peut procéder
à la détermination des effets marginaux de la moyenne ou des
effets marginaux moyens pour cerner l'information centralisée. L'effet
marginal de la variable ?????? sur le niveau
SAWADOGO Israel-- ISE 3-- ENSAE
MARAHASA/DPPO-BF
36
Barrières et opportunités à
l'adoption des techniques de CES/DRS au Burkina Faso, dans la zone
sahélienne
d'inefficacité au niveau de l'individu i est
déterminée par :???? (????) ???????? =
????,??v2/?? ????,?? . On détermine
ainsi l'effet marginal moyen (????(????)) et l'effet
marginal de l'individu moyen ????(????) . Pour le cas
???????? ????????
particulier de la variable d'intérêt, adoption des
CES/DRS, l'effet marginal moyen est donnée par :
(?????? ??????/?????? ?? ????(????) ) =
????,??????/?????? v2/???? ? ????,??
??=1 avec ???? ??????/?????? la variable dichotomique "adoption
des
techniques de CES/DRS" et ????,??????/?????? le coefficient qui
lui est associé.
Cas où le terme d'inefficacité suit une
loi normale tronquée: hypothèse de la nullité du
paramètre ?? rejetée
Dans ce cas, la prise en compte des variables influençant
la variance du terme d'efficacité technique ne peut se faire sans
prendre en compte cette influence sur le paramètre (Parmeter et
Kumbhakar, 2014).
???? ???_ ?,?? =????,?? ????
{
???? ???2 ?,??=????,?? ???? , ? ??=1, ... ,??
???? = ????,??
????
Dans ce cas de figure, les effets marginaux pour une variable
explicative k donnée au niveau de l'individu i sont :
|
????(????)
??????,?? (??)
|
= ??????(1 - ????????-
????2) + ??????????,??((1 +
????2)????+ ????????2)/2
|
|
????????(????)
??????,?? (??)
|
????
= ??
????,??
|
????(?? (????)2 - ??????(????)) + [1 - 21 ????(???? +
????3 + ????(2 + 3????2) +
2????????2)]
|
|
Où ???? = ????
????,??
|
?? (????
, ???? = ??(????) et ?????? (respectivement ??????)
représente le coefficient associé à la variable
|
k expliquant la moyenne ?? (respectivement la variance du terme
u).
Apres une description de la méthode de
détermination de l'effet du choix d'adoption sur l'inefficacité
technique, il convient de faire un développement sur le type de
technologie utilisé pour l'estimation de la frontière
stochastique de production.
SAWADOGO Israel-- ISE 3-- ENSAE
MARAHASA/DPPO-BF
37
Barrières et opportunités à
l'adoption des techniques de CES/DRS au Burkina Faso, dans la zone
sahélienne
III.3.3 Type de technologie utilisé pour la
détermination de la frontière
Selon les développements faits dans la
littérature (Kinane, 2002 ; albouchi et al,(2002)), les fonctions Cobb
Douglas et translog paraissent mieux adaptées à la
modélisation d'une frontière de production dans le domaine
agricole. Ces fonctions le seront donc pour la détermination de la
frontière de production dans notre cas. Cependant l'utilisation d'une
fonction translog serait limitée lorsqu'on dispose d'un grand nombre
d'intrants entrant dans la construction de la frontière de production.
La forme analytique de la fonction Cobb Douglas pour p intrants est
donnée par :
p p
??????????(x,f3) = f30 ? xj ???? s??it In ??????????(x, f3) =
In f30 + ? f3j In xj
j=1 j=1
Avec f3j représentant le coefficient
associé à la quantité de l'intrant xj
Présentation des variables utilisées dans
l'analyse par frontière de production
Les intrants
Les intrants disponibles pour cette étude sont
regroupés dans le tableau suivant, les valeurs sont ramenées
à la superficie en hectare.
Tableau 3: variables décrivant la
production agricole
Variables Unités
Production
Rendement : production par hectare kg/ha
Intrants
Semences kg/ha
Engrais chimiques et organiques
Fumure organique kg/ha
Urée g/ha
Npk g/ha
Herbicides liquide L/ha
Fongicides g/ha
Nombre d'actifs agricoles Nombre d'actifs/hectare
Source: construction de l'auteur, manuel de
l'enquêteur
La variable utilisée pour capter la production est le
rendement. Le rendement pour une exploitation
et concernant une culture
donnée désigne la quantité produite par unité de
surface. Dans le cadre
SAWADOGO Israel-- ISE 3-- ENSAE
MARAHASA/DPPO-BF
38
Barrières et opportunités à
l'adoption des techniques de CES/DRS au Burkina Faso, dans la zone
sahélienne
de cette étude, la superficie sera
évaluée en hectare (ha) et la production en kilogramme (kg). Ce
qui nous donne un rendement en kg/ha. Quant aux intrants utilisés dans
la construction de frontière de production, Les quantités
utilisées sont toute converties en quantité par superficie. On
distingue principalement 4 catégories d'intrants utilisées par
les agriculteurs de production agricole au Burkina Faso.
? Les semences : La quantité de semence utilisée
au niveau de l'exploitation agricole, quantifiée en kg/ha. Une
distinction est faite entre les semences améliorées et les
semences locales.
? Les engrais chimiques et organiques : les engrais sont
évalués en quantité utilisée par hectare. L'engrais
organique désigne la fumure organique et les engrais chimiques
désignent le NPK et l'urée.
? Les substances phytosanitaires : les herbicides et les
fongicides. Les fongicides sont des substances utilisées pour lutter
contre les champignons s'attaquant aux plantes.
? Le travail : cet intrant est pris en compte à travers
le nombre d'actifs agricoles du ménage exploitant. Il s'agit en effet du
nombre de membres du ménage, dont l'activité principale est
agricole.
Variables expliquant
l'hétéroscédasticité
Les variables utilisées pour expliquer la variance de
l'efficacité technique sont les modalités de la gestion de la
surface exploitée (les techniques de CES/DRS et le labour) et les
caractéristiques sociodémographiques du responsable de cette
gestion. L'analyse de la moyenne et de la variance de l'inefficacité
technique permettra de déterminer l'effet de ces variables sur le niveau
d'efficacité technique des agriculteurs.
SAWADOGO Israel-- ISE 3-- ENSAE
MARAHASA/DPPO-BF
39
Barrières et opportunités à
l'adoption des techniques de CES/DRS au Burkina Faso, dans la zone
sahélienne
| 


