Déterminants des investissements directs étrangers en France.

Annexe 3 : Corrélations des variables

Corrélation de Spearman (autre version)

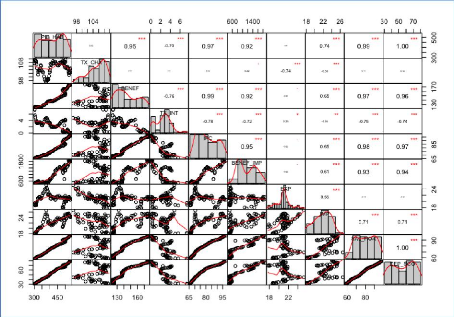
Tests de Spearman pour les variables corrélées

					SPEARMAN'S RANK CORRELATION RHO
					Data : PIB HAB and DEP SCO
S =		420			P-Value < 2,2e-16
					Alternative hypothesis : true rho is not equal to 0
					Rho = 0,994
				SPEARMAN'S RANK CORRELATION RHO
				Data : SAL_HOR and DEP_SCO
S =			0	P-Value < 2,2e-16
				Alternative hypothesis : true rho is not equal to 0
				Rho = 1
					SPEARMAN'S RANK CORRELATION RHO
					Data : PIB HAB and SAL HOR
S =		420			P-Value < 2,2e-16
					Alternative hypothesis : true rho is not equal to 0
					Rho = 0,994

89

									SPEARMAN'S RANK CORRELATION RHO
									Data : PIB_HAB and IPC
S =	437,01								P-Value < 2,2e-16
									Alternative hypothesis : true rho is not equal to 0
									Rho = 0,994
										SPEARMAN'S RANK CORRELATION RHO
										Data : BENEF and IPC
S = 1		439,1								P-Value < 2,2e-16
										Alternative hypothesis : true rho is not equal to 0
										Rho = 0,980
							SPEARMAN'S RANK CORRELATION RHO
							Data : IPC and SAL_HOR
S =					13		P-Value < 2,2e-16
							Alternative hypothesis : true rho is not equal to 0
							Rho = 1
											SPEARMAN'S RANK CORRELATION RHO
											Data : BENEF and SAL HOR
S = 1		402,6									P-Value < 2,2e-16
											Alternative hypothesis : true rho is not equal to 0
											Rho = 0,981
							SPEARMAN'S RANK CORRELATION RHO
							Data : IPC and DEP_SCO
S =					13		P-Value < 2,2e-16
							Alternative hypothesis : true rho is not equal to 0
							Rho = 1
										SPEARMAN'S RANK CORRELATION RHO
										Data : IPC and BENEF_IMP
S = 5				717,1						P-Value < 2,2e-16
										Alternative hypothesis : true rho is not equal to 0
										Rho = 0,922
											SPEARMAN'S RANK CORRELATION RHO
											Data : PIB HAB and BENEF
S = 1			864,6								P-Value < 2,2e-16
											Alternative hypothesis : true rho is not equal to 0
											Rho = 0,974
											SPEARMAN'S RANK CORRELATION RHO
											Data : BENEF and DEP_SCO
S = 1		402,6									P-Value < 2,2e-16
											Alternative hypothesis : true rho is not equal to 0
											Rho = 0,981

90

		SPEARMAN'S RANK CORRELATION RHO
		Data : BENEF_IMP and DEP_SCO
S = 5	690	P-Value < 2,2e-16
		Alternative hypothesis : true rho is not equal to 0
		Rho = 0,922

J'ai réalisé le test de Spearman pour l'ensemble des variables dont la corrélation était supérieure ou égale à 0,95. Comme dans l'ensemble des cas, la p-value est inférieure à 0,05, les variables sont donc corrélées positivement et significativement au seuil de risque de 1%.

Annexe 4 : Régressions linéaires multiples du modèle

Dans cette première partie de l'annexe, nous avons réalisé les graphiques de la première régression (« reg1 »).

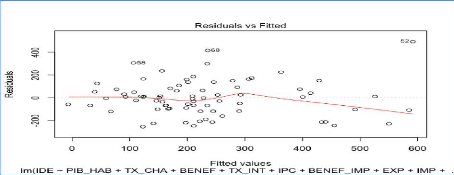
Analyse de l'homoscédasticité des résidus du modèle reg1

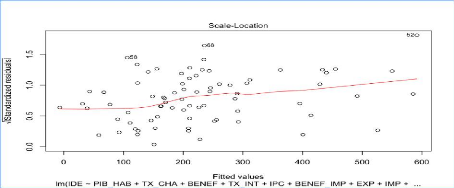
Analyse de la forme fonctionnelle du modèle reg1

91

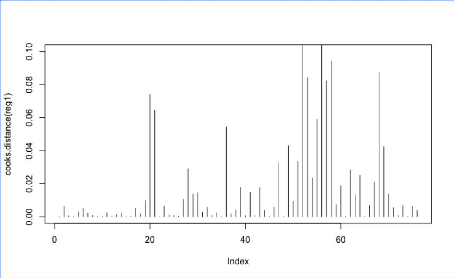
Analyse des informations qui influencent l'information du modèle reg1

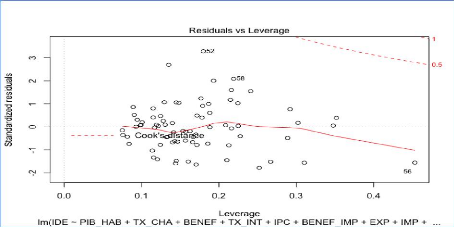
Distance de Cooks du modèle reg1

92

Nous allons poursuivre avec les graphiques du modèle de régression linéaire 1 semi logarithmique (« reg1sl »).

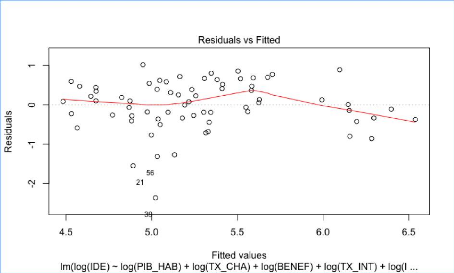
Analyse de l'homoscédasticité des résidus du modèle reg1sl

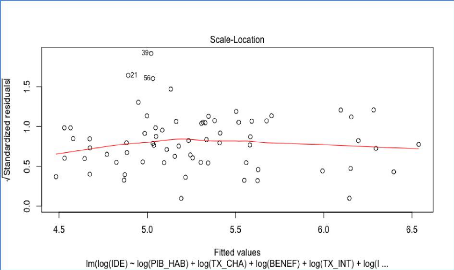
Analyse de la forme fonctionnelle du modèle reg1sl

93

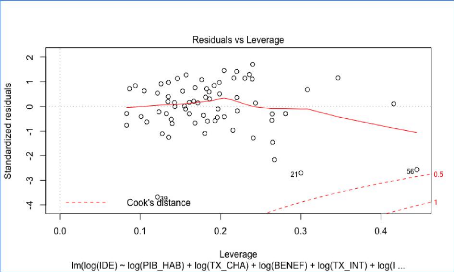
Analyse des informations qui influencent l'information du modèle reg1sl

Analyse de la normalité des résidus du modèle reg1sl

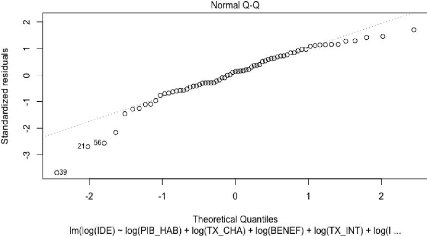
94

Nous allons poursuivre avec les graphiques du modèle de régression linéaire 2 (« reg2 »).

Analyse de l'homoscédasticité des résidus du modèle reg2

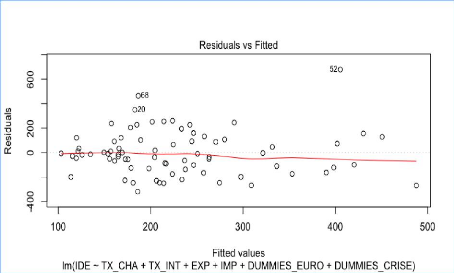
Analyse de la forme fonctionnelle du modèle reg2

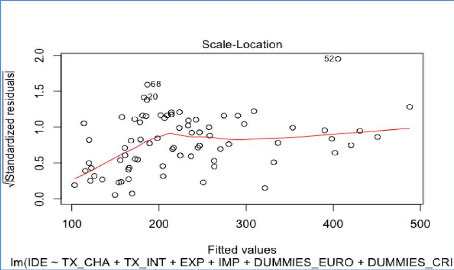
Analyse des informations qui influencent l'information du modèle reg2

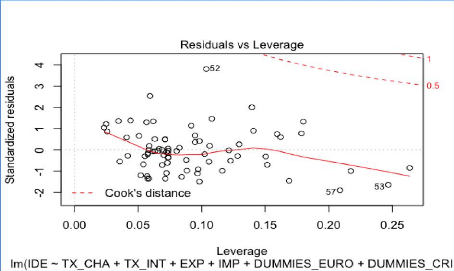
95

Analyse de la normalité des résidus du modèle reg2

96

Les graphiques suivants sont ceux du modèle de régression linéaire 2 semi logarithmique (« reg2sl »).

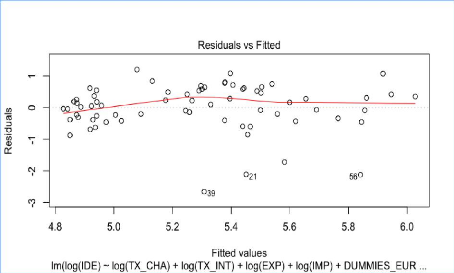
Analyse de l'homoscédasticité des résidus du modèle reg2sl

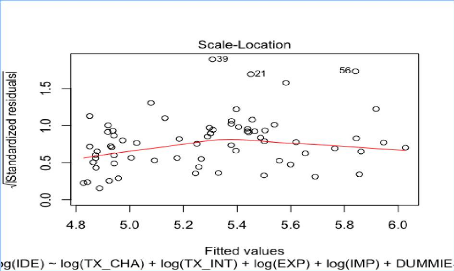
Analyse de la forme fonctionnelle du modèle reg2sl

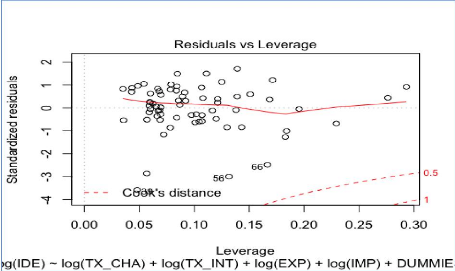
Analyse des informations qui influencent l'information du modèle reg2sl

97

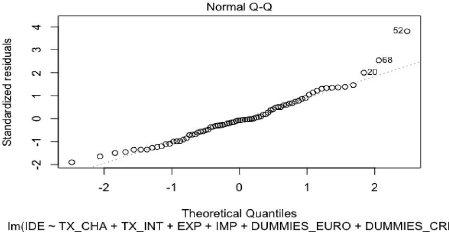
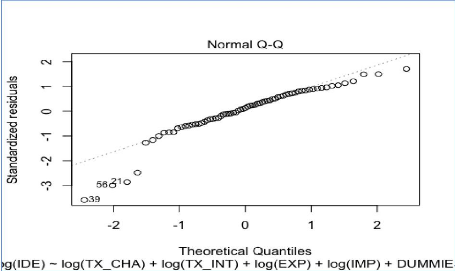
Analyse de la normalité des résidus du modèle reg2sl

98

Nous allons poursuivre avec les graphiques du modèle de régression linéaire 3 (« reg3 »).

Analyse de l'homoscédasticité des résidus du modèle reg3

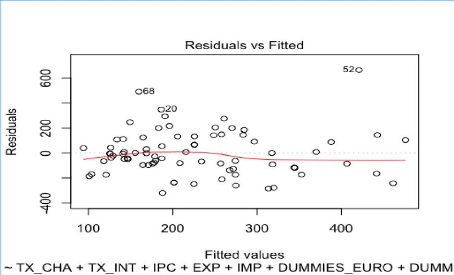
Analyse de la forme fonctionnelle du modèle reg3

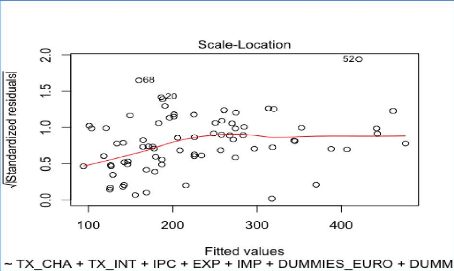
Analyse des informations qui influencent l'information du modèle reg3

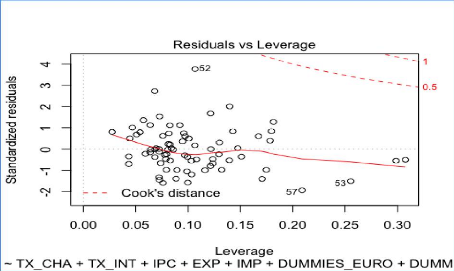
99

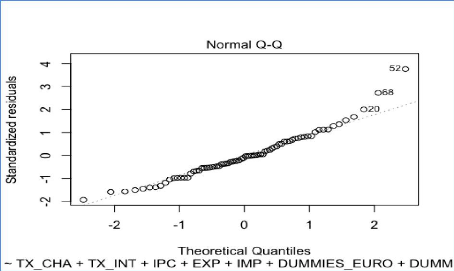
Analyse de la normalité des résidus du modèle reg3

100

Enfin, nous allons terminer avec les graphiques du modèle de régression linéaire 4 (« reg4 »).

Analyse de l'homoscédasticité des résidus du modèle reg4

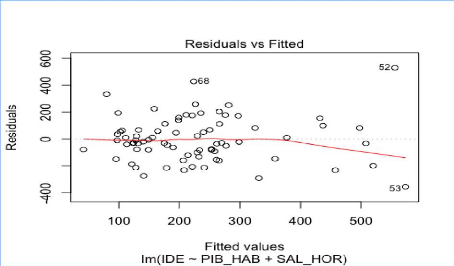
Analyse de la forme fonctionnelle du modèle reg4

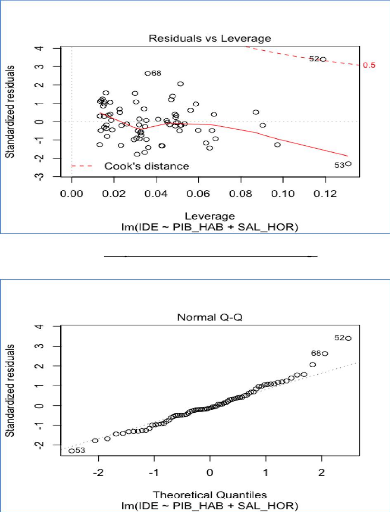
Analyse de la normalité des résidus du modèle reg4

101

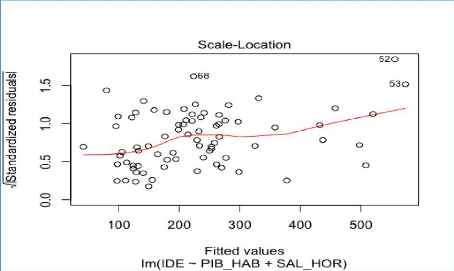
Analyse des informations qui influencent l'information du modèle reg4

102