Annexes du mémoire
Annexe 1 : Présentation des variables pour la
base « Ide »
Nature des variables du modèle
|
Variables
|
Type de
variable
|
1ère
valeur
|
2ème
valeur
|
3ème
valeur
|
4ème
valeur
|
5ème
valeur
|
|
IDE
|
Numérique
|
100
|
91,1
|
118,6
|
199,3
|
144,3
|
|
PIB_HAB
|
Numérique
|
302
|
304
|
306
|
307
|
311
|
|
TX CHA
|
Numérique
|
1,35
|
1,35
|
1,33
|
1,34
|
1,3
|
|
BENEF
|
Numérique
|
124
|
124
|
124
|
126
|
125
|
|
TX INT
|
Numérique
|
7,44
|
7,37
|
5,62
|
5,01
|
4,04
|
|
IPC
|
Numérique
|
65,8
|
65,8
|
66
|
66,3
|
66,4
|
|
BENEF_IMP
|
Numérique
|
468
|
491
|
499
|
506
|
525
|
|
EXP
|
Numérique
|
18,9
|
19,4
|
18,7
|
18,9
|
19,4
|
|
IMP
|
Numérique
|
18,1
|
18,3
|
18,2
|
18,1
|
18,7
|
|
SAL HOR
|
Numérique
|
58,4
|
58,9
|
59,1
|
59,3
|
59,8
|
|
DEP_SCO
|
Numérique
|
30,5
|
30,9
|
31,3
|
31,8
|
32,2
|
|
DUMMIES_EURO
|
Numérique
|
0
|
0
|
0
|
0
|
0
|
|
DUMMIES CRISE
|
Numérique
|
0
|
0
|
0
|
0
|
0
|
Le tableau ci-dessus permet de connaître la nature des
variables du modèle. Nous voyons très clairement que l'ensemble
des variables sont quantitatives sauf les variables DUMMIES_EURO et
DUMMIES_CRISE. Par conséquent, il a fallu les recoder car ces deux
variables étaient qualitatives et non des variables numériques.
Enfin, ce tableau a été obtenu à l'aide de la fonction
str sur le logiciel R Studio.
Histogrammes de fréquences de chaque variable
quantitative
80
81
82
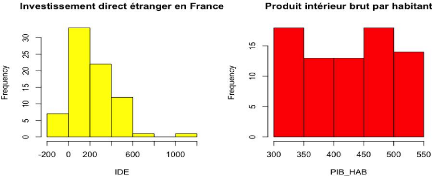
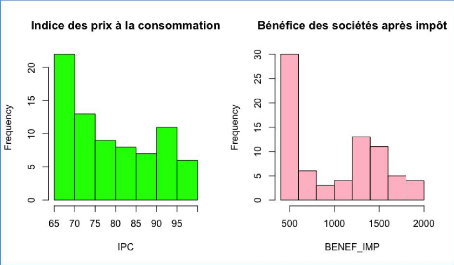
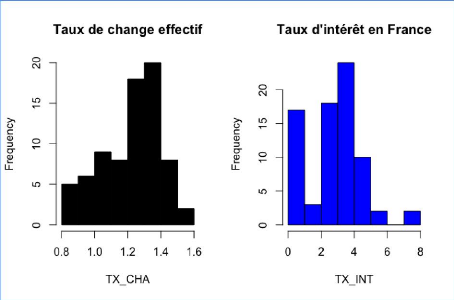
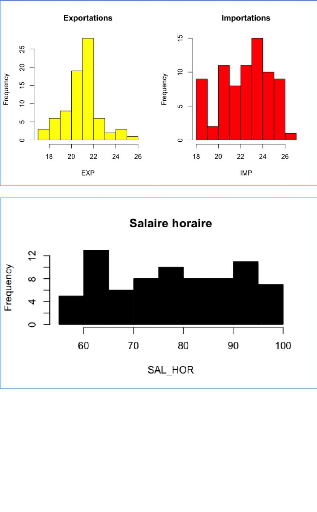
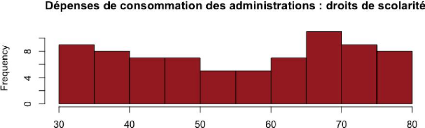
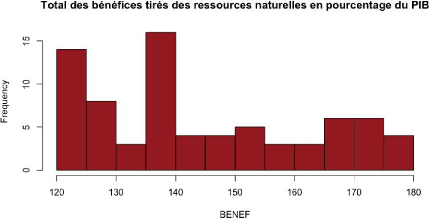
Les histogrammes ci-dessus représentent chaque variable
quantitative. Par exemple, dans le cas de l'IDE, la fréquence la plus
élevée (environ 35) est obtenue pour une valeur de l'IDE comprise
entre 0 et 200.
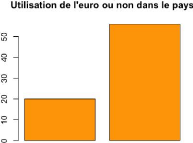
Dans le cas des variables DUMMIES_EURO et DUMMIES_CRISE qui
sont des variables qualitatives (binaire), nous avons réalisé des
diagrammes en barre afin de les représenter.
83
Diagramme en barre de chaque variable qualitative
Annexe 2 : Valeurs atypiques du modèle
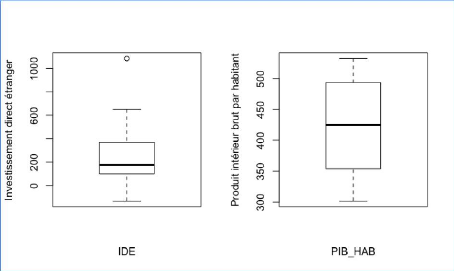
Cette deuxième annexe a pour but de déterminer
les éventuelles valeurs atypiques pour chaque variable du modèle.
Deux tests sont effectués en fonction du nombre de valeurs atypiques :
test de Grubbs dans le cas où une seule observation est potentiellement
atypique et le test de Rosner dans le cas où au moins deux observations
sont potentiellement atypiques.
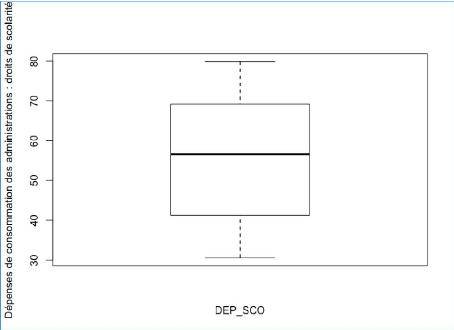
Boxplot de chaque variable quantitative
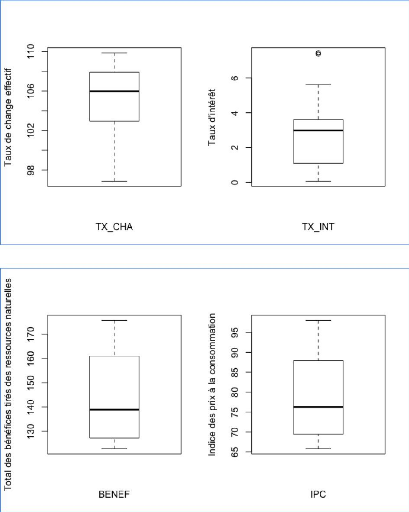
84
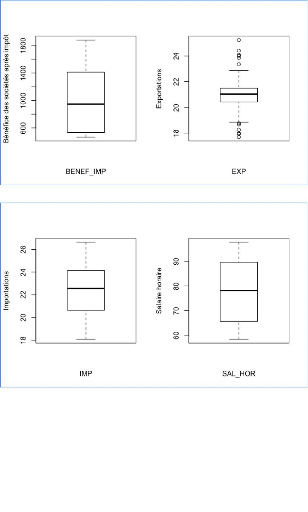
85
Test de Grubbs pour la variable IDE
GRUBBS TEST FOR ONE OUTLIER
Data : Ide$IDE
G = 4,2573
U = 0,7551
P-Value = 0,0004
86
Pour la variable IDE, la p-value du test de Grubbs est
inférieure à 0,05 et donc par conséquent,
l'hypothèse H0 est refusée au seuil de risque de 5%. La variable
IDE a donc une valeur atypique.
Suppression de l'observation atypique
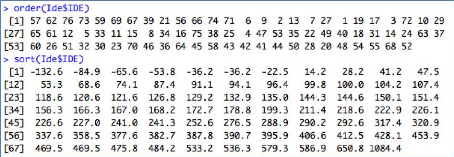
87
D'après le tableau ci-dessus, on observe que la valeur
atypique correspond donc à la cinquante-deuxième observation. Il
s'agit du quatrième trimestre 2007.
Test de Rosner pour la variable TX INT
|
NUMERO
|
OUTLIERS
|
TEST STATISTIQUE
|
CRITICAL VALEUR
|
|
1
|
1
|
2,883
|
3,288
|
|
2
|
2
|
3,034
|
3,283
|
|
3
|
3
|
2,089
|
3,278
|
|
4
|
1
|
1,749
|
3,273
|
|
5
|
2
|
1,674
|
3,268
|
|
6
|
3
|
1,688
|
3,263
|
|
7
|
1
|
1,652
|
3,257
|
|
8
|
2
|
1,694
|
3,252
|
|
9
|
3
|
1,738
|
3,247
|
|
10
|
1
|
1,788
|
3,241
|
|
11
|
2
|
1,837
|
3,236
|
|
12
|
3
|
1,848
|
3,230
|
Dans le test de Rosner, si le test statistique est
supérieur à la critical valeur alors l'observation sera
considérée comme atypique. Dans le cas ou ce test est
inférieur, l'observation ne sera pas atypique. Pour la variable TX_INT,
il n'y a pas de valeurs potentiellement atypiques.
Test de Rosner pour la variable EXP
|
NUMERO
|
OUTLIERS
|
TEST STATISTIQUE
|
CRITICAL VALEUR
|
|
1
|
1
|
2,922
|
3,288
|
|
2
|
2
|
2,532
|
3,283
|
|
3
|
3
|
2,425
|
3,278
|
|
4
|
1
|
2,482
|
3,273
|
|
5
|
2
|
2,498
|
3,268
|
|
6
|
3
|
2,548
|
3,263
|
|
7
|
1
|
2,506
|
3,257
|
|
8
|
2
|
2,586
|
3,252
|
|
9
|
3
|
2,484
|
3,247
|
|
10
|
1
|
2,442
|
3,241
|
|
11
|
2
|
2,280
|
3,236
|
|
12
|
3
|
2,296
|
3,230
|
Pour la variable EXP, il n'y a pas de valeurs potentiellement
atypiques car le test statistique est inférieur à la critical
valeur pour l'ensemble des observations.
88
|
|



