V.2 Application économétrique du
modèle
V.2.1 Premier modèle étudié
Tout d'abord, le premier modèle réalisé
prendra en compte l'ensemble des variables étudiées dans ce
dossier.
Tableau 4 : Régression linéaire 1 nommée
« reg1 »
|
Variables
|
Estimate
|
Std.Error
|
T value
|
Pr (>|t|)
|
Significativité
|
|
CONSTANTE
|
4 375,503
|
1 545,775
|
2,831
|
0,006
|
**
|
|
PIB HAB
|
23,240
|
7,370
|
3,153
|
0,002
|
**
|
|
TX_CHA
|
-232,620
|
321,811
|
-0,723
|
0,472
|
|
|
BENEF
|
31,368
|
19,606
|
1,600
|
0,115
|
|
|
TX INT
|
-33,420
|
35,409
|
-0,944
|
0,349
|
|
|
IPC
|
-50,686
|
34,077
|
-1,487
|
0,142
|
|
|
BENEF IMP
|
0,168
|
0,201
|
0,838
|
0,405
|
|
|
EXP
|
-82,262
|
61,951
|
-1,328
|
0,189
|
|
|
IMP
|
26,216
|
48,838
|
0,537
|
0,593
|
|
|
SAL HOR
|
-192,080
|
88,030
|
-2,182
|
0,033
|
*
|
|
DEP_SCO
|
30,742
|
42,371
|
0,726
|
0,471
|
|
|
DUMMIES EURO
|
135,249
|
178,332
|
0,758
|
0,451
|
|
|
DUMMIES_CRISE
|
-63,550
|
104,478
|
-0,608
|
0,545
|
|
|
Valeur
|
|
Multiple R-squared
|
0,427
|
|
Adjusted R-squared
|
0,318
|
|
F-statistic
|
3,919
|
|
P-value
|
0,000
|
D'après le tableau 4, nous remarquons que la
qualité du modèle semble correcte mais pas suffisante. En effet,
le coefficient de détermination (R2) est de 0,427. Cela
signifie qu'environ 42,7% de la variance de l'IDE est expliquée par les
variables explicatives choisies.
65 CREPON B. et JACQUEMET N. « Econométrie :
méthode et applications ». Chapitre 2. Page 46.
Consulté le 19 février 2019.
66 BOURBONNAIS R. « Econométrie ».
Dunod. 9ème édition. Consulté le 19
février 2019.
47
La constante est significative au seuil de risque de 1%. La
variable PIB_HAB est également significative au seuil de risque de 1%.
Lorsque le PIB_HAB augmente d'une unité, l'IDE augmente de 23,240
dollars. La croissance du PIB_HAB et les IDE sont fortement
corrélés positivement. En effet, l'augmentation des IDE dans un
pays est supérieure à sa croissance économique.
L'augmentation des IDE d'une économie va permettre de manière
générale de pouvoir produire plus, donc d'augmenter la
productivité afin de créer de l'emploi, ce qui va
améliorer le niveau de vie et donc le PIB par habitant. Concernant la
variable SAL_HOR, cette dernière est significative au seuil de risque de
5%. On peut donc dire que lorsque le SAL_HOR augmente d'un point, l'IDE baisse
de 192,080 dollars. L'un des objectifs principaux des IDE est de réduire
ses coûts de production, et donc d'investir dans les pays ou les zones
dans lesquels les coûts sont plus faibles que ceux où l'entreprise
est implantée. Ainsi, les entreprises gagnant en productivité
à moindre coût dans les pays moins strict en matière de
fiscalité vont pouvoir répartir une partie de ses gains dans les
salaires. On peut donc voir que les entreprises étrangères
pratiquant des IDE dans un pays proposeront un salaire plus élevé
à ses employés que les entreprises locales. Les IDE ont donc un
impact positif sur les salaires qu'ils augmentent. Enfin, l'hypothèse H0
selon laquelle au moins une des variables explicatives à un impact
significatif permet d'accepter le test de Fisher car la p-value est de 0,000 et
elle est donc bien inférieure à 0,05.
Tableau 5 : Test des résidus du modèle «
reg1 »
|
MODELE
|
SHAPIRO-WILK
|
BREUSCH-PAGAN
|
RAMSEY
|
|
Reg1
|
W = 0,963
p-value = 0,026
|
BP = 22,431
p-value = 0,033
|
RESET = 0,428
p-value = 0,654
|
D'après le test de Shapiro-Wilk dans le cadre du
premier modèle de régression, l'hypothèse H0 de
normalité des résidus est refusée car la p-value est
inférieure à 0,05. On va donc modifier la forme fonctionnelle du
modèle en passant par une estimation semi-logarithmique. Le test de
Breusch-Pagan permet de vérifier l'hypothèse
d'homoscédasticité des résidus. Dans ce modèle, on
refuse l'hypothèse d'homoscédasticité des résidus
au seuil de risque de 5% pour l'unique raison que la p-value est
inférieure à 0,05. Nous allons essayer de résoudre cela
par l'estimation d'un modèle semi-logarithmique. Enfin, le test de
Ramsey permet de vérifier la linéarité du modèle.
Ce test ne permet cependant pas d'en déduire s'il
48
s'agit du meilleur modèle à estimer. Dans notre
cas, la forme fonctionnelle linéaire du modèle
spécifié est acceptée au seuil de 5% car la p-value du
test est de 0,654, ce qui est supérieure à 0,05. Par
conséquent, on accepte l'hypothèse H0 au seuil de risque de
5%.
Tableau 6 : VIF du modèle « reg1 »
|
VARIABLE
|
VIF
|
|
PIB_HAB
|
824,854
|
|
TX_CHA
|
8,635
|
|
BENEF
|
322,454
|
|
TX_INT
|
9,487
|
|
IPC
|
340,665
|
|
BENEF_IMP
|
25,014
|
|
EXP
|
22,299
|
|
IMP
|
31,677
|
|
SAL_HOR
|
3274,557
|
|
DEP_SCO
|
1162,316
|
|
DUMMIES_EURO
|
17,036
|
|
DUMMIES_CRISE
|
4,010
|
La Variance Inflation Factor (VIF) permet de juger la
colinéarité entre les variables explicatives du modèle.
L'ensemble de nos variables sauf DUMMIES_CRISE, TX_CHA et TX_INT ont de la
forte colinéarité car leurs valeurs dépassent 10.
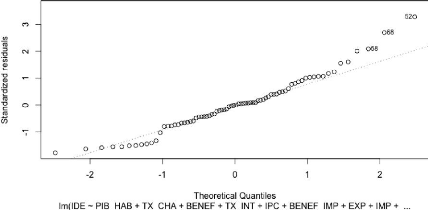
Graphique 19 : Analyse de la normalité des
résidus
49
Ce modèle ne semble pas très satisfaisant. Les
différents tests confirment ce que l'on peut supposer au vu du graphique
19. A priori la loi normale n'est pas suivie (il faut supprimer les
observations 58, 68 et 52). Le modèle présente des
problèmes au niveau de la normalité des résidus (test de
Shapiro-Wilk). Le test de Breusch-Pagan a indiqué que le modèle
refuse l'hypothèse d'homoscédasticité des résidus.
La forme fonctionnelle du modèle va donc être modifiée en
passant par un modèle semi-logarithmique. D'après le VIF, nous
avons un souci de multicolinéarité. En revanche le modèle
ne présente pas de problème de forme fonctionnelle (test de
Ramsey). Les différents graphiques de ce modèle (reg1) ainsi que
les distances de Cooks se trouvent en fin de dossier (annexe 4).
A présent, nous allons procéder à
l'étude du modèle semi-logarithmique. Ce modèle sera
réalisé avec les mêmes variables. Nous allons seulement
tester le logarithme de ces variables.
Tableau 7 : Régression semi-logarithmique 1
nommée « reg1sl »
|
Variables
|
Estimate
|
Std.Error
|
T value
|
Pr (>|??|)
|
Significativité
|
|
CONSTANTE
|
7,695
|
30,838
|
0,250
|
0,804
|
|
|
Log(PIB HAB)
|
12,678
|
16,384
|
0,774
|
0,442
|
|
|
Log(TX CHA)
|
-2,090
|
1,693
|
-1,235
|
0,222
|
|
|
Log(BENEF)
|
26,373
|
12,051
|
2,188
|
0,033
|
*
|
|
Log(TX INT)
|
0,417
|
0,285
|
1,462
|
0,149
|
|
|
Log(IPC)
|
-3,991
|
13,951
|
-0,286
|
0,776
|
|
|
Log(BENEF IMP)
|
1,283
|
0,735
|
1,744
|
0,087
|
.
|
|
Log(EXP)
|
0,515
|
6,788
|
0,076
|
0,940
|
|
|
Log(IMP)
|
-3,701
|
5,273
|
-0,702
|
0,486
|
|
|
Log(SAL HOR)
|
-60,322
|
25,713
|
-2,346
|
0,022
|
*
|
|
Log(DEP_SCO)
|
17,810
|
9,283
|
1,919
|
0,060
|
.
|
|
DUMMIES EURO
|
0,126
|
0,742
|
0,169
|
0,866
|
|
|
DUMMIES_CRISE
|
0,160
|
0,506
|
0,316
|
0,753
|
|
|
Valeur
|
|
Multiple R-squared
|
0,388
|
|
Adjusted R-squared
|
0,257
|
|
F-statistic
|
2,961
|
|
P-value
|
0,003
|
D'après le tableau 7, nous observons que la
qualité explicative du modèle s'est légèrement
dégradée. Le coefficient de détermination est de 0,388.
Nous pouvons donc dire que 38,8% de la variance de l'IDE est expliquée
par les variables explicatives choisies. En revanche, les variables BENEF et
SAL_HOR ont un impact significatif au seuil de risque de 5% sur l'IDE. Par
exemple, lorsque le BENEF augmente d'un point, l'IDE augmente de
50
log(26,373). Les IDE des entreprises, principalement celle
étant dans des pays ou des zones à forte pression fiscale
facilite l'investissement dans des pays où le contrôle fiscal est
bien moins important et ainsi avoir une plus grande productivité pour
des coûts réduits et de ce fait, faire des économies
d'échelles. A travers les IDE, les entreprises essaient d'augmenter
leurs bénéfices. Les variables BENEF_IMP et DEP_SCO ont un impact
significatif au seuil de risque de 10% sur l'IDE. Par exemple, lorsque les
DEP_SCO augmente d'une unité, l'IDE augmente de log(17,810). Soulignons
que le fonctionnement de l'éducation national étant très
liée à tout ce qui est de l'ordre des collectivités, leurs
budgets provenant ainsi de l'Etat, des régions et des
départements. Le niveau d'éducation favorisant à long
terme la croissance, l'augmentation des IDE dans un pays et l'imposition
auxquels ils sont soumis, permet à l'Etat et aux collectivités
territoriales d'augmenter leur budget et ainsi d'avoir la possibilité de
le réinvestir dans l'éducation. Les résultats de
l'éducation étant eux aussi bénéfiques aux IDE
à moyen et long terme. De plus, dans les pays à forte
fiscalité, les IDE permettent d'échapper à l'impôt
car étant tourné vers des pays où la fiscalité est
moins contraignante. En effet, plus un pays recevra des IDE, moins il devra
mettre en place une politique de fiscalité lourde pour éviter une
baisse de ceux-ci. Ainsi, les IDE devrait avoir un impact positif sur les
bénéfices après impôts avec des marges plus
importantes pour les entreprises ayant investis dans un pays afin de moins
payer d'impôts. On est donc en contradiction avec ce que l'on avait
supposé dans la partie économique. Elle peut vendre au même
prix avec les impôts en moins ce qui lui permet de faire plus de
bénéfices. Enfin, le test de Fisher est accepté car la
p-value est inférieure à 0,05. Soulignons que les
résultats obtenus avec le premier modèle semi-logarithmique sont
différents du modèle linéaire multiple. Le modèle
logarithmique semble donc différent.
Tableau 8 : Test des résidus du modèle «
reg1sl »
|
MODELE
|
SHAPIRO-WILK
|
BREUSCH-PAGAN
|
RAMSEY
|
|
Reg1sl
|
W = 0,936
p-value = 0,0012
|
BP = 10,962
p-value = 0,532
|
RESET = 3,694
p-value = 0,031
|
Dans ce modèle, nous constatons que l'hypothèse
H0 de normalité des résidus est refusée (d'après le
test de Shapiro-Wilk). De plus, la forme fonctionnelle linéaire du
modèle spécifié est rejetée au seuil de 5%
(d'après le test de Ramsey). En revanche, l'hypothèse
51
d'homoscédasticité des résidus est
acceptée au seuil de risque de 5% (d'après le test de
Breusch-Pagan). Les différents graphiques de ce modèle (reg1sl)
se trouvent en fin de dossier (annexe 4).
Tableau 9 : VIF du modèle « reg1sl »
|
VARIABLE
|
VIF
|
|
PIB_HAB
|
1236,555
|
|
TX_CHA
|
9,730
|
|
BENEF
|
262,280
|
|
TX_INT
|
13,129
|
|
IPC
|
420,234
|
|
BENEF_IMP
|
18,021
|
|
EXP
|
30,771
|
|
IMP
|
41,682
|
|
SAL_HOR
|
2360,907
|
|
DEP_SCO
|
1056,814
|
|
DUMMIES_EURO
|
16,588
|
|
DUMMIES_CRISE
|
4,648
|
Dans ce modèle, l'ensemble des variables sauf TX_CHA et
DUMMIES_CRISE ont de la forte colinéarité car leurs valeurs
dépassent 10.
L'ensemble des graphiques de ce modèle se trouve en fin
de dossier (annexe 4). Ce modèle semi-logarithmique est très
similaire au modèle de régression 1 (reg1). Cependant, il semble
moins bon à cause des différents tests effectués. Dans ce
dernier, plus de variables sont ressorties significatives. Nous allons à
présent étudier un nouveau modèle qui ne prendra pas en
compte les variables corrélées fortement négativement
à la variable TX_INT. Ce modèle ne prendra donc pas en compte les
variables PIB_HAB, BENEF, IPC, BENEF_IMP, SAL_HOR et DEP_SCO.
|
|



