III. Modélisation des dépôts à
vue 1. Description statistiques.
L'analyse des dépôts à vue
constitués dans les livres des banques est effectuée sur la
période allant de 2000 à 2009. Les données
financières sont issues essentiellement de la Banque Centrale
élaborées à partir des reporting effectués par les
banques. Elles sont établies sur une base trimestrielle, en vue de se
caler sur la périodicité du dispositif prudentiel, et reparties
selon la nature du bénéficiaire. Les principales
catégories de bénéficiaires sont les
sociétés d'Etat et EPIC, les Particuliers et les Entreprises
privées et les autres déposants.
Figure 7: Evolution des
dépôts à vue 2000-2009.
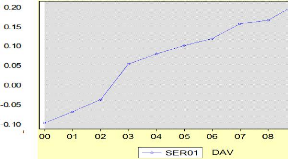
Source : calcul de l'auteur sur EVIEWS
Les dépôts à vue, constitués dans
les livres des banques ont enregistré sur la période sous revue,
une évolution très fluctuante qui reflète le rythme de
constitution et de retrait des dépôts. Le taux de croissance
trimestriel maximal enregistré sur la période est ressorti
à 16% et a été observé en décembre 2009. En
revanche, la baisse la plus importante est de 5% et a été
observée en septembre 2001. Sur la période, le taux de croissance
moyen est ressorti à 11%, traduisant ainsi une consolidation des
dépôts à vue, en rapport avec l'accroissement de
l'activité économique. Les retraits sur les dépôts
à vue ont été plus prononcés sur la période
allant de septembre 2007 à décembre 2009.
Tableau 8: Résumé
des statistiques descriptives de la série des taux de variation des
dépôts agrégés
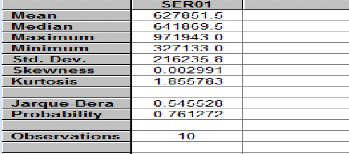
Source : Calcul de l'auteur sur Eviews
NB : La statistique observée
permet de vérifier l'hypothèse de normalité de la
série, c'est-à-dire si la série suit une loi normale ou
non. S'agissant des coefficients de dissymétrie (Skewness) et
d'aplatissement (Kurtosis), ils permettent d'étudier l'étalement
de la série par rapport à la moyenne qui détermine
toujours le degré de normalité.
2. Modélisation des dépôts à
vue agrégés (DAVA) Figure 8. Modélisation
DAVA
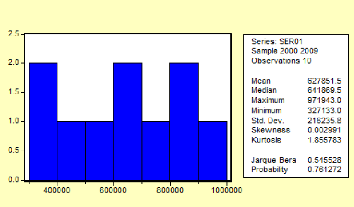
Source : calcul de l'auteur sur EVIEWS
3. 
Détermination du modèle
corrélogramme. Figure 9 : Corrélogramme
observée
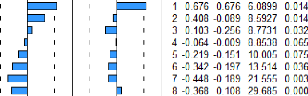
Source : calcul de l'auteur, d'après
données BCEAO
Il apparaît que Q-stat (rang 08) a une probabilité
critique, car étant supérieure à 5% donc le résidu
suit un processus de brut blanc.
4. Régression tendancielle
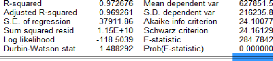
Source : auteur après calcul sur EVIEWS
5. Vecteur autorégression
estimé
Figure 10 : Autorégression
DAV


Source : auteur après calcul sur EVIEWS
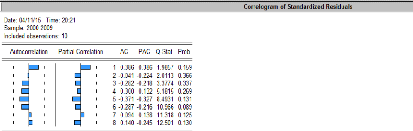
Figure 11 : Corrélogramme
observée

Source : auteur après calcul sur EVIEWS
La croissance rapide de l'autocorrélogramme et la variance
de l'autocorrélogramme partielle à partir du premier rang permet
d'identifier un processus AR (1)
6. Test sur le résidu du modèle
MA(1)
Figure 12 :
Corrélogramme observée sur modèle MA

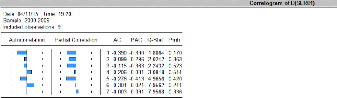

70
Source : auteur après calcul sur EVIEWS
7. Test sur le résidu du modèle AR(1)
Figure 13: Corrélogramme observée
modèle AR
Source : auteur après calcul sur
EVIEWS
8. Test sur le résidu du modèle ARMA(1)
Figure 14: Corrélogramme observée sur
modèle ARMA
Source : auteur après calcul sur EVIEWS

71
Il ressort que les résidus des trois modèles sont
tous des bruits blancs, leur probabilité de Q-stat étant
supérieure à 5%. En conséquence, il conviendrait de
retenir le modèle qui présente les meilleures
caractéristiques en termes de prévision.
9. Test de Ljung-Box Q :
Ce modèle doit suivre un processus de bruit blanc.
Autrement dit, l'espérance mathématique de son résidu est
nulle. On compare la probabilité du Q-stat pour le dernier terme avec le
seuil critique de 5%. Sur le résidu du modèle AR(1)
Figure 15: Corrélogramme
observée
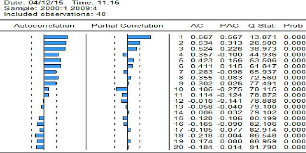
Source .
· calcul auteur sur EVIEW,
d'après données BCEAO
Il apparaît que Q-stat a une probabilité
critique inférieure au seuil critique de 5% donc le résidu ne
suit pas un processus de brut blanc.
16. Sur le résidu du modèle
MA(4)
Figure 15: Corrélogramme
observée
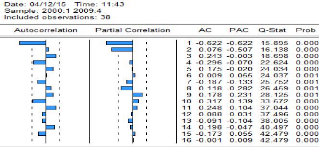
Source .
· calcul auteur sur EVIEW,
d'après données BCEAO

72
Q-stat à une probabilité critique
inférieure au seuil critique de 5% donc le résidu ne suit pas un
processus de brut blanc.
Figure 16: Diagramme en
bande Q-Stat
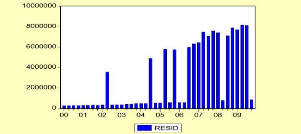
Source .
· calcul auteur sur EVIEW,
d'après données BCEAO
Q-stat a une probabilité critique inférieure au
seuil critique de 5% donc le résidu ne suit pas un processus de brut
blanc.
Figure 17: Etude du taux de croissance
des dépôts à vue agrégés entre 2000 et
2009
Source .
· calcul auteur sur EVIEW,
d'après données BCEAO Figure 18: résidu DAV

Source .
· calcul auteur sur EVIEW,
d'après données BCEAO

73
Cette représentation vise à apprécier le
degré de stabilité du modèle. A la différence des
tests précédents, c'est une étude graphique qui permet de
se prononcer sur le degré de stabilité du modèle.
| 


