II.3. NOTION DE CORRÉLATION
La régulation peut aussi être comme l'ensemble des
techniques visant à contrôler une grandeur et la maintenir
à un niveau préféré.
Pour arriver à ce niveau voulu que nous pouvons appeler
consigneconsigneconsigne, il faut identifier les facteurs pouvant influencer la
variable à réguler. Nous pouvons comprendre cette
réflexion à partir de cette petite illustration: pour augmenter
ou diminuer le volume d'une musique, celui qui veut le faire doit identifier
l'organe de la radio qu'il peut manipuler et le volume du son varie.
De même avec notre travail, nous devons identifier la
variable que l'État peut manipuler et faire varier le prix du maïs
sur le marché de la ville de Kananga. C'est pour cette raison que nous
faisons appel à la notion de corrélation.
A) DÉFINITION
Soient x et y deux grandeurs statistiques quantitatives
observées. On souhaite:
(1) Déterminer s' il existe une relation entre x et y;
(2) Caractériser la forme de la relation entre x et y
(positive ou négative, monotone ou non monotone)
(3) Quantifier la valeur de la liaison.
B. La covariance:
La covariance est l'espérance des produits des variables
centrés. Soit COV (x, y) ={[X-E (x)] [Y-E (Y)]}.
Son objectif est de quantifier la liaison entre deux variables x
et y de manière à mettre en évidence le sens de la
liaison et son intensité.
La covariance mesure la tendance de deux variables à
être simultanément au-dessus ou en-dessous de leurs
espérance mathématique.
Il est trouvé par la formule suivante:
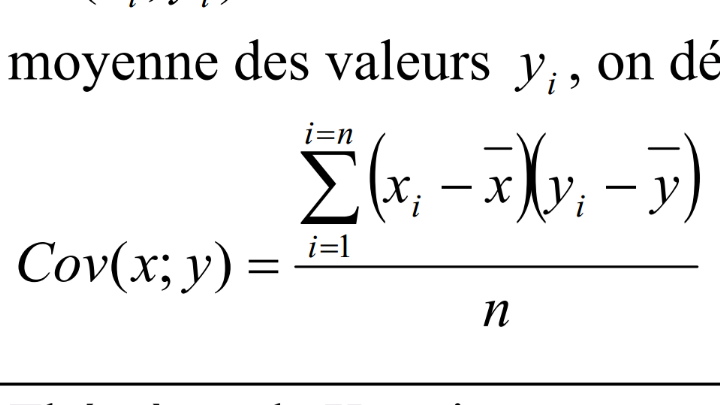
_
Où X est la moyenne de Xi qui est la somme des Xi
rapportée au nombre des Xi.
Et Y est la moyenne de Yi qui est la somme des Yi
rapportée au nombre des Yi.
Remarques:
Si COV (x, y) > 0 la rellation est positive, c'est à
dire que lorsque x est supérieur à son espérance
mathématique (ou moyenne arithmétique), vice-versa.
Si COV (x, y) = 0 : il n'y a pas de rellation monotone; pas
d'interdépendance entre variables.
Si COV (x, y) < 0 : la liaison est négative. C'est
à dire que quand x est plus grand que son espérance
mathématique, Y a tendance à être plus petit que son
espérance mathématique.
C) le coefficient de corrélation
le coefficient de corrélation est la normalisation de la
covariance par le produit des ecarts types des variables. Il constitue une
mesure de liaison linéaire de deux variables.
Il est trouvé par la formule suivante:
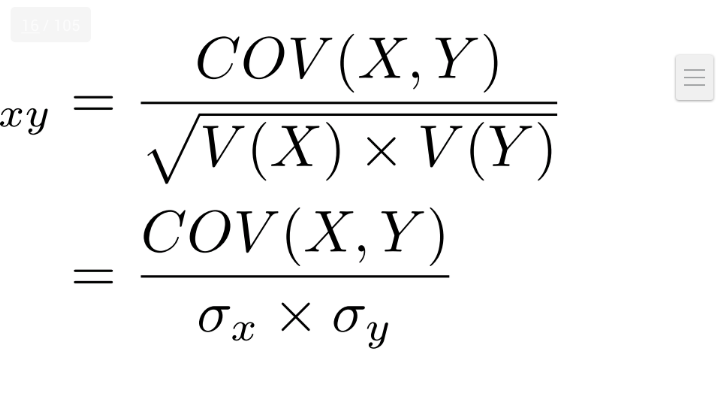
Ce coefficient prend toujours une valeurs supérieurs ou
égale à 1 et inférieur ou égale à 0. Soit 1
< r (x, y) > 0
Si r (x, y) > 0 les deux variables varient dans le même
sens. L'augmentation de l'un entraîne l'augmentation de l'autre.
Si r (x, y) < 0 les deux variables varient dans les sens
opposés. L'augmentation de l'entraîne la diminution de l'autre.
Si r (x, y) = 0 les variables sont indépendantes.
Si r (x, y) = 1 la corrélation est parfaite, positive et
linéaire.
Si r (x, y) = -1 la corrélation est parfaite,
négative et linéaire.
| 


