1.5.1 Test de validation d'une prévision
Un test de validation d'une prévision est un test dont
l'hypothèse nulle revient à postuler que la prévision est
issue du processus générateur de données ou DGP des
données.
La validitéde la prévision d'une grandeur
économique est évaluée en comparant sa réalisation
ex-post à la valeur prédite ex-ante.
Ainsi, l'évaluation de la VaR est
généralement fondée sur des tests statistiques des deux
principales hypothèses que le processus associéaux violations de
la VaR anticipée doit satisfaire, à savoir l'hypothèse de
couverture non conditionnelle et l'hypothèse d'indépendance.
1.5.2 Violations de la VaR
On appelle violation (ou hit, ou exception) une situation dans
laquelle à la date t la perte observée excède la VaR
anticipée. De plus, on appelle hit function, ou hit variable, la
variable indicatrice It(c) associée à
l'observation ex-post d'une violation de la VaR à c% à
la date t.
It(c) = 1 si rt < V
aRt|t_1(c) (1.5)
It(c) = 0 sinon. (1.6)
Exemple de simulation de 5000 valeurs de la loi
skewlaplace et Backtesting sur les 1000 dernières valeurs
> library(PerformanceAnalytics)
> library(quantmod)
> library(rugarch)
> library(car)
> library(FinTS)
11
> library(GeneralizedHyperbolic)
> rt <-rskewlap(5000, mu = 0.0000321, alpha = 1/23,
beta = 1/22)
> # convertir la simulation en time series (pour
l'adapter au backtesting)
> x.Date <- as.Date("2003-02-01") + c(1:5000)
> ret <- zoo(rt, x.Date)
> # backtesting unconditional VaR models
> # normal VaR, HS and modified HS
> #
>
> # set up estimation window and testing window
> n.obs = length(ret)
> w.e = 4000
> w.t = n.obs - w.e
> alpha = 0.95
> # loop over testing sample, compute VaR and record hit
rates > backTestVaR <- function(x, p = 0.95) {
+ normal.VaR = as.numeric(VaR(x, p=p,
method="gaussian"))
+ modified.VaR = as.numeric(VaR(x, p=p,
method="modified"))
+ ans = c(normal.VaR, modified.VaR)
+ names(ans) = c("Normal", "Modified")
+ return(ans)
+ }
> # rolling 1-step ahead estimates of VaR
> VaR.results = rollapply(as.zoo(ret), width=w.e,
+ FUN = backTestVaR, p=0.95, by.column = FALSE,
+ align = "right")
> VaR.results = lag(VaR.results, k=-1)
> chart.TimeSeries(merge(ret, VaR.results),
legend.loc="topright",main="Backtesting")
12
Backtesting
2003-02-02 2006-02-01 2009-02-01 2012-02-01 2015-02-01
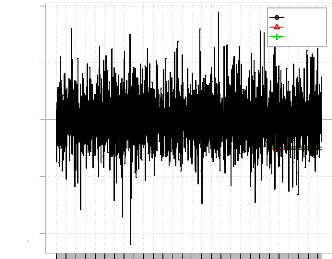
Value
-0.4 -0.2 0.0 0.2 0.4
ret Normal Modified
Les violations, sur les 1000 derniers rendements, de la VaR
Normale et de la VaR Cornish-Fisher sont sur les 2 graphiques qui suivent
> par(mfrow=c(1,2))
> # Show Normal VaR violations
> normalVaR.violations = as.zoo(ret(index(VaR.results),
]) < VaR.results(, "Normal"]
> violation.dates.normal =
index(normalVaR.violations(which(normalVaR.violations)])
> # plot violations
> plot(as.zoo(ret(index(VaR.results),]), col="blue",
ylab="Return",main="Violations normal VaR")
> abline(h=0)
> lines(VaR.results(, "Normal"], col="black",
lwd=2)
> lines(as.zoo(ret(violation.dates.normal,]), type="p",
pch=16, col="red", lwd=2)
> # Show modified VaR violations
> modifiedVaR.violations =
as.zoo(ret(index(VaR.results), ]) < VaR.results(, "Modified"]
> violation.dates.modified =
index(modifiedVaR.violations(which(modifiedVaR.violations)])
> # plot violations
> plot(as.zoo(ret(index(VaR.results),]), col="blue",
ylab="Return",main="Violations modified VaR")
> abline(h=0)
> lines(VaR.results(, "Modified"], col="black",
lwd=2)
> lines(as.zoo(ret(violation.dates.modified,]),
type="p", pch=16, col="red", lwd=2)
Violations normal VaR
|
Return
|
-0.2 -0.1 0.0 0.1 0.2 0.3
|
|
2014 2015 2016
Index
Violations modified VaR
|
Return
|
-0.2 -0.1 0.0 0.1 0.2 0.3
|
|
2014 2015 2016
Index
13
Une prévision de VaR est valide si et seulement si la
séquence des violations satisfait les deux hypothèses suivantes
:
/L'hypothèse de couverture non
conditionnelle
/L'hypothèse d'indépendance
hypothèse de couverture non
conditionnelle
L'hypothèse de couverture non conditionnelle est
satisfaite lorsque la probabilitéque se réalise ex -post une
perte en excès par rapport à la VaR anticipée ex-ante est
précisément égale au taux de couverture c .
Pr[It(c) = 1] = E[It(c) = 1] = c (1.7)
Exemple
Pour une VaR à 1% utilisée comme mesure de
référence sur 500 périodes, l'espérance du nombre
de violations doit être égale à 5. Si le nombre de
violations est significativement supérieur ou inférieur à
5 %, la mesure de VaR est non valide.
hypothèse d'indépendance
L'hypothèse d'indépendance des violations est
satisfaite lorsque les violations de la VaR observées à deux
dates différentes pour un même taux de couverture doivent
être indépendamment distribuées. Formellement, la variable
It(c) associée à la violation à la date t de la
VaR pour un taux de couverture à c%, est indépendante de
la variable It_k(c),Vk =6 0.
14
hypothèse de couverture conditionnelle
L'hypothèse de couverture conditionnelle est satisfaite
lorsque la probabilitéconditionnelle à l'infor-mation disponible
en t-1 se réalise ex-post une perte en excès par rapport à
la VaR est préciséme nt égale au taux de couverture c
:
Pr[It(c) = 1|I~t_1] =
E[It(c)|1~t_1] = c (1.8)
oùI~t_1 désigne l'ensemble
d'information utilisépour prévoir la VaR.
A noter que l'hypothèse de couverture conditionnelle
implique l'hypothèse de couverture non conditionnelle et
l'hypothèse d'indépendance.
| 


