1.3Estimation des
paramètres du Tobit
Le modèle Tobit admis est justifié par la fait
que seulement la modalité 3= travail bénévole de la
variable dépendante (statut dans l'emploi) nous intéresse, il
s'agit donc de faire une censure à gauche et une à droite. La
fonction de Vraisemblance d'un tel modèle s'écrit :
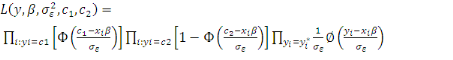 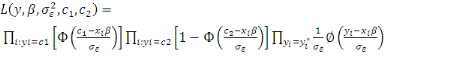 (7) (7)
Le premier terme désigne le produit des
probabilités que les observations yi prennent lesvaleurs de censures
inférieures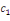 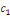 : :
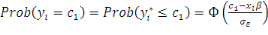 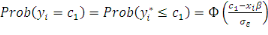 (8)
(8)
Le second terme désigne le produit des
probabilités que les observations yi prennent lesvaleurs de censures
supérieures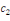 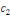 : :
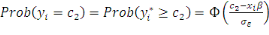 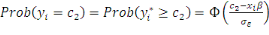 (9)
(9)
Pour mesurer la qualité d'ajustement des modèles
estimés, nous considérons plusieurs indicateurs classiques qui
sont le critère d'information d'Akaike (AIC) [Akaike, 1974], le
critère d'information bayésien (BIC) [Schwarz, 1978], la P-value
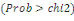
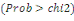 habituellement utilisée dans les modèles logit et le
pseudoR2de McFadden (McFadden, 1974) :
habituellement utilisée dans les modèles logit et le
pseudoR2de McFadden (McFadden, 1974) :
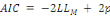
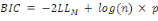
R2de McFadden = 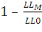 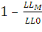
AvecLLMla log-vraisemblance, p le
nombre de paramètres à estimer du modèle, n la
taille de l'échantillon et LL0 la log-vraisemblance
du modèle nul (sans autre paramètre que la constante ou
modèle par défaut). Il est formulé comme suit :
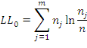
Où nj et ndésignent
respectivement les effectifs de la modalité jet l'effectif
total de l'échantillon. L'AIC et le BIC permettent de pénaliser
les modèles en fonction du nombre de paramètres afin de
satisfaire le critère de parcimonie, la pénalité
étant encore plus grande avec le BIC. Plus ces critères sont
faibles, meilleur est le modèle. Le R2 de McFadden,
ou pseudo-R2, a été construit pour ressembler
au R2 de la régression linéaire mais doit
s'interpréter en termes de part de déviance et non en termes de
part de variance. Bien que compris entre 0 et 1 (comme le
R2),des simulations ont montré qu'une valeur autour
de 0,3 correspond à une valeur élevée de
R2(Domencich and McFadden [1975, p. 134-135]).
Un autre indicateur de la littérature
économétrique pour juger de la qualité de l'estimation
avec le Tobit est le test de rapport de vraisemblance formulé comme
suit :
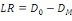
Avec 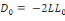 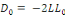 la
déviance du modèle par défaut et la
déviance du modèle par défaut et 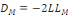 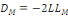 la
déviance du modèle d'étude. L'indicateur du test du
rapport de vraisemblance suit une loi de Khi-deux définie par : la
déviance du modèle d'étude. L'indicateur du test du
rapport de vraisemblance suit une loi de Khi-deux définie par :
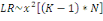
Avec 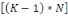 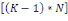 le
degré de liberté où K est le nombre de paramètres
à estimer et N, le nombre de modalités de la variable
dépendante. Le modèle est de bonne qualité si la valeur
calculée est supérieure à la valeur donnée par la
table de Khi-deux à un seuil á fixé. le
degré de liberté où K est le nombre de paramètres
à estimer et N, le nombre de modalités de la variable
dépendante. Le modèle est de bonne qualité si la valeur
calculée est supérieure à la valeur donnée par la
table de Khi-deux à un seuil á fixé.
L'estimateur du Maximum de Vraisemblance (MV) nécessite
la vérification de deux principales hypothèses pour l'estimation
des modèles Tobit. Il s' agit des hypothèses
d'hétéroscédasticité et de normalité.
De façon générale, on montre que
l'estimateur du MV en présence
d'hétéroscédasticité est asymptotiquement
biaisé. L'importance des biais asymptotiques croît avec le
degré de censure des données. Greene (1997) propose d'utiliser un
test du multiplicateur de Lagrange. Une expression de la statistique LM du test
de l'hypothèse nulle d'homoscédasticité H0 : á = 0
est
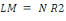 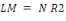 , qui
suit une distribution , qui
suit une distribution 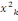 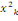
Où N désigne le nombre d'observations et
où R2 est le coefficient de détermination de la régression
du vecteur unitaire 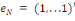 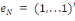 de
dimension (N, 1) sur les K+P +1 colonne de la matrice de
dimension (N, 1) sur les K+P +1 colonne de la matrice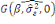 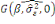 . .
LM = 0. 2183* 9037 = 1972,7771,
Cette valeur est très supérieure à la
valeur tabulée 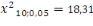 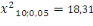 donc
l'hypothèse H0 est acceptée, il y a bien
homoscédasticité. donc
l'hypothèse H0 est acceptée, il y a bien
homoscédasticité.
La seconde principale hypothèse qui peut affecter de
façon sensible les propriétés de l'estimateurdu MV est
l'hypothèse de non normalité des perturbations. Nous utilisons un
test de Schapiro-Wilk dont la formule est :
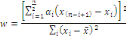
La statistique W peut donc être
interprétée comme le coefficient de détermination (le
carré du coefficient de corrélation) entre la série des
quantiles générées à partir de la loi normale et
les quantiles empiriques obtenues à partir des données. Plus
W est élevé, plus la compatibilité avec la loi
normale est crédible. Le w obtenu est : 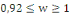 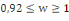 pour
chacune des variables. On conclue sur l'hypothèse nulle de
normalité des perturbations. pour
chacune des variables. On conclue sur l'hypothèse nulle de
normalité des perturbations.
La stratégie de test à la Hausman (1978) :
Nelson (1981), Melenberg et Van Soest(1996), plus complexe mais plus
approprié conduit à la même conclusion. Le travail
d'estimation avec le Maximum de vraisemblance peut être effectué
en toute quiétude.
| 


