7.2.4 Les valeurs propres
Une valeur propre est un indicateur à traves lequel on
peut mesurer l'apport en pourcentage de l'information (inertie) apportée
par les différentes variables sur un axe factoriel.
Alhassane G. Abdoulaziz Page
Elève Ingénieur Statisticien 40
Promotion 2008-2011
7.2.4.1 Tableau des valeurs propres.
Tableau des valeurs propres
|
Trace de la matrice:
|
7.00000
|
|
|
Numéro
|
Valeur
propre
|
Pourcentage
|
Pourcentage cumulé
|
|
1
|
1,7341
|
24,77
|
24,77
|
|
2
|
1,1831
|
16,90
|
41,67
|
|
3
|
1,0146
|
14,49
|
56,17
|
|
4
|
0,8778
|
12,54
|
68,71
|
|
5
|
0,8292
|
11,85
|
80,55
|
|
6
|
0,7122
|
10,17
|
90,73
|
|
7
|
0,6491
|
9,27
|
100,00
|
Ici, le premier axe factoriel explique lui seul 24,77% de
l'information (l'inertie) totale apportée par les différentes
variables. Les trois premiers axes détiennent eux seuls, plus de la
moitié de l'information totale.
Selon la norme standard, on conseille d'archiver au moins 80% de
l'inertie total. Donc nous allons considérer cinq(5) axes car ayant
pourcentage cumulé de l'inertie=80,55.
7.2.4.2 Tableau : Test des valeurs propres
Intervalles palladiens d'Anderson (seuil:
|
0.95)
|
|
|
|
|
Numéro
|
Borne
inférieure
|
Valeur
propre
|
Borne
supérieure
|
|
1
|
1,6844
|
1,7341
|
1,7838
|
|
2
|
1,1492
|
1,1831
|
1,2170
|
|
3
|
0,9856
|
1,0146
|
1,0437
|
|
4
|
0,8526
|
0,8778
|
0,9029
|
|
5
|
0,8054
|
0,8292
|
0,8529
|
Dans le tableau précédent, aucune borne ne
contient un zéro, donc nous pouvons dire qu'au seuil de 5%, toutes les
valeurs propres sont significativement différentes de zéro.
Alhassane G. Abdoulaziz Page
Elève Ingénieur Statisticien 41
Promotion 2008-2011
7.2.4.3 Digramme des valeurs propres.

2,0000
1,5000
1,0000
0,5000
0,0000
1,7341
1,1831
1 2
eboulie des valeurs propres
1,0146
3 4 5
0,8778 0,8292
Valeur propre
Sources : base de données 2010 INS.
Ce diagramme nous montre la valeur de l'information que
détient chaque axe.
Alhassane G. Abdoulaziz Page
Elève Ingénieur Statisticien 42
Promotion 2008-2011
7.2.5 Cercle de corrélation des variables
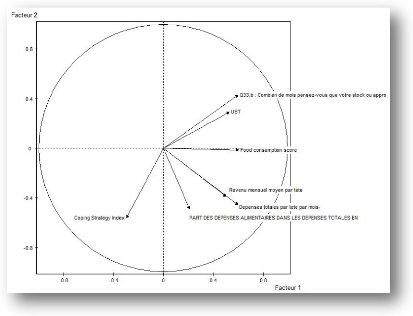
Dans ce cercle de corrélation on constate que la
variable indice
stratégie de survie (CSI) est bien projetée
sur l'axe 4 car ayant un cosinus
carré qui est égale à
0,398 et son coordonné sur l'axe n°4 est égale
à
0,63. Cette variable a contribuée à 45,36% à
la formation de cet axe. La
variable revenu mensuel par tête et les
variables dépense total mensuelle
par tête sont
corrélées entre elles. Les cosinus carrés de ces
dernières sont
respectivement 0,433 et 0,354 et ont
contribuées respectivement à la
formation des axes n°5
(52,22%) et l'axe n°3 (20,42%). Cependant, la
variable revenu mensuel
par tête est bien représentée dans le plan
factoriel que
la variable dépense mensuelle par tête.
52,22% est la contribution de la variable score de
consommation à la formation de l'axe n°5. Cette variable a pour
coordonnée - 0,65 sur l'axe n°5 et son cosinus carré est
égale à 0,433. L'individu moyen est la variable dépense
totale par mois car ayant le plus faible cosinus carré(0,269).
Les coordonnées des différentes variables sont
mises en annexe (1, 2,3).
Alhassane G. Abdoulaziz Page
Elève Ingénieur Statisticien 43
Promotion 2008-2011
Vue toutes ces caractéristiques, nous pouvons dire que
les ménages de notre population échantillon seront classés
en cinq(5) sous-groupes.
|
|



