II.2.2. PRESENTATION DU MODELE DE BASE THEORIQUE
Il nous sera question dans cette partie de présenter,
la méthode d'analyse, le modèle d'interprétation de la
méthode proposée, les différents tests choisis, ainsi que
la présentation du modèle.
1) Modèle théorique
d'estimation
Avant tout, il sied de rappeler que la performance constitue
notre variable dépendante, en termes de l'objectif atteint par
l'organisation.
Cela étant, nous ferons recours aux modèles
logit polytomiques non ordonnés, qui
constituent une famille de modèles économétriques
adaptés au cas où la variable à expliquer est une variable
qualitative, dont les modalités ne peuvent être classées
les unes par rapport aux autres. A cet égard, nous pouvons dire que la
variable à expliquer qui est la performance dans le cas de notre
étude a plus de deux modalités d'où elle est
polytomique.
2) Présentation du modèle
théorique
A ce stade, il convient d'attirer l'attention sur le
flottement terminologique qui existe dans la littérature. Boskin(1974) a
dénommé son modèle loit conditionnel, alors que Schmidt et
Strauss(1975) ont appelé le leur logit multinomial. Cette distinction
coïncide en fait avec la nature des variables explicatives retenues dans
l'une et l'autre modélisation. Celles du modèle de Boskin sont
des caractéristiques des choix offerts, alors que celles du
modèle de Schmidt et Strauss sont des caractéristiques des
individus qui choisissent. Ce sont les dénominations que nous adopterons
dans le document du moins dans un premier temps. Elles ne font cependant pas
l'unanimité. En réalité, nous verrons que ces deux
modèles « purs » sont deux cas particuliers d'un modèle
logit qui rassemble des variables explicatives caractérisant les choix
et les variables explicatives décrivant les individus ; c'est
plutôt la dénomination de multinomial qui lui sera
réservée.
31
3) Définition des modèles logit multinomial
et logit conditionnel a. Le modèle logit multinomial
On observe un échantillon de n individus, répartis
en J catégories disjointes. Chaque individu i appartient à une
catégorie j parmi les J possibles. Il est décrit par un ensemble
de K caractéristiques xi1, xi2, ..., xik (par exemple son âge,
sexe, niveau d'études, etc).

Le modèle est construit sur l'idée suivante : La
probabilité que l'individu i, compte tenu de ses caractéristiques
xik, fasse partie de la catégorie j est supposée dépendre
des xik, ou, plus précisément d'une combinaison linéaire
des xik. Formellement, cela s'écrit :
Le vecteur est le vecteur (ligne) des variables explicatives du
modèle.
Sa première composante vaut systématiquement 1.
Elle prend en compte dans le modèle, le fait que les
catégories n'ont pas les mêmes effectifs. On remarquera que les
paramètres de la combinaison linéaire dépendent de la
catégorie j.
On note le vecteur (colonne) de ces paramètres. Le
problème
est de trouver une forme fonctionnelle G telle que chaque
quantité P (j/xi) soit bien une probabilité, c'est-à-dire
possède les propriétés suivantes :
Pour assurer la stricte positivité de P (j/xi), on prend
la fonction exponentielle. C'est ce choix qui fonde le modèle logit. On
pose donc :
Mais cette quantité peut prendre des valeurs
supérieures à 1. On la nomme alors par la
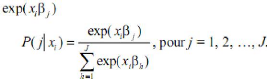
somme des , et le modèle s'écrit de la
manière suivante : (2)
32
La forme fonctionnelle donnée par (2) répond
bien aux propriétés (1). Le modèle possède a priori
un nombre relativement élevé de paramètres : (K+1) x J. En
l'état, les effets des caractéristiques x sur
l'appartenance à l'une des J catégories ne sont pas
identifiés (on dit aussi que le modèle n'est pas
identifié, ou que les paramètres ne le sont pas). En effet,
supposons que l'on ajoute un terme quelconque aux J
paramètres , un terme aux J
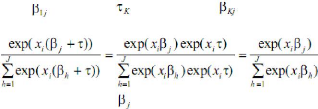
paramètres ,..., un terme aux J paramètres . On a
alors, en notant
Une infinité de valeurs de est donc possible, qui
conduit à une même valeur de la
probabilité. Il faut alors imposer aux
paramètres une condition qui permet l'identification du modèle.
Celle qui est retenue en règle très générale est
d'imposer la nullité de tous les paramètres relatifs à une
catégorie donnée appelée alors catégorie de
référence. Si on décide que la catégorie de
référence correspond à j = J, alors la condition
d'identification est :
Avec cette condition identifiante, le modèle
s'écrit finalement de la manière suivante :
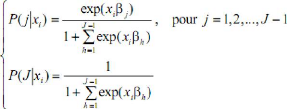
On a parfois intérêt à écrire le
modèle sous une forme plus facile à manier. En divisant P (j/xi)
par P (J/xi) et en prenant le logarithme, on obtient :
On notera qu'avec J = 2, on retrouve l'expression d'un logit
dichotomique. On peut aisément changer de catégorie de
référence. Prenons j = 1, par exemple comme nouvelle
référence. En utilisant (4), on a :
33
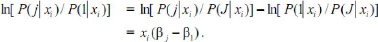
Les « nouveaux » paramètres s'obtiennent par
différence des anciens. Plus généralement, j1 et j2
étant deux catégories quelconques, on a :
Le rapport des deux probabilités ne dépend pas
des catégories autres que f1 et f2 On notera une autre
propriété intéressante du modèle. Puisque deux
catégories sont disjointes,
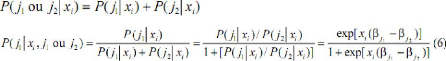
Ainsi, conditionnellement au fait que i appartient aux
catégories f1 ou f2, la probabilité P (j1/xi)
est modélisée par un logit dichotomique de paramètre
Cette propriété se traduit, sur le plan
pratique, par le fait qu'on peut estimer les paramètres d'un logit
multinomial en menant plusieurs estimations de logit dichotomiques opposant une
catégorie à chacune des (J-1) autres. Seule la précision
des paramètres estimés diffère (Begg et Gray, 1984).
| 


