II.5. Spectroscopie
UV-VISIBLE
On exprime l'absorbance par la loi de Lambert-Beer
par : A= ålc
Où å est le coefficient
d'extinction molaire.
Les mesures d'absorbance effectuées ont
été tirées d'un spectrophotomètre de marque
GENESY 20 thermo Spectrum.
II.5.1. Evaluation de la
stabilité photochimique et thermique
1° Principe de la méthode
Les essais de stabilités photochimiques et thermiques
sont respectivement réalisés en exposant les extraits au
rayonnement UV et la chaleur. Lors de la dégradation, la molécule
passe de l'état natif (forme naturelle) à l'état
dégradé (structure décomposée).
Cette décomposition de la
molécule a pour conséquence la modification de la composition du
milieu et de ses propriétés physico-chimiques, notamment son
absorption.
Les anthocyanes sont des molécules facilement
modifiables par des paramètres physico-chimiques. La modification de
l'absorption par la solution des anthocyanes est exploitée en
spectrophotométrie UV-Visible pour étudier sa
dégradation.
Mode opératoire
Ø Préparer 5 mg/ml de la solution aqueuse des
extraits d'anthocyanes et le placer dans les tubes à essai.
Ø Exposer à la lumière UV (365 nm)
à différentes longueurs d'ondes pendant des intervalles des temps
différents ou à l'étuve MEMMERT à
différentes températures la solution préparée.
Ø Après les traitements de la solution, mesurer
les absorbances pour chaque solution traitée.
2° Modèle théorique de la cinétique
de dégradation thermique des anthocyanes
La dégradation des anthocyanes, sous l'action de la
chaleur, peut être considérée comme une réaction
chimique au cours de laquelle une molécule d'anthocyane A
est décomposée irréversiblement, en une ou
plusieurs molécules désignées par
B selon le schéma suivant :
 (II-1) (II-1)
Où k est la constante de
vitesse.
La réaction de la dégradation est une
réaction de décomposition. Elle est d'ordre 1 et son
équation de vitesse est donnée par :
 (II-2) (II-2)
Où CA, k et t sont
respectivement la concentration de A, la constante de vitesse et le
temps de dégradation. En résolvant cette équation
différentielle on obtient :
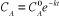 (II-3) (II-3)
Avec 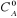 la concentration initiale de A. la concentration initiale de A.
A la longueur d'onde où seule l'espèce
A absorbe, l'équation de Lambert-Beer s'écrit :
 (II-4) (II-4)
Alors
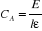 (II-5) (II-5)
et  (II-6) (II-6)
La combinaison des équations (II-3), (II-4), (II-5) et
(II-6) donne :
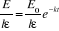 (II-7) (II-7)
E
O
t
Eo
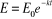 (II-8) (II-8)
Figure II-1: Evolution de
E en fonction de temps d'exposition à la chaleur selon la
relation II-8
Mais il se peut que le produit de dégradation absorbe
également à la même longueur d'onde que A. Dans ce
cas, l'équation de Lambert-Beer peut s'écrire
 (II-9) (II-9)
 (II-10) (II-10)
où
 (II-11)
(II-11)
 (II-12) (II-12)
où

on peut écrire

avec
 (II-13) (II-13)
où

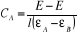 (II-14) (II-14)
Tenant de (14), l'équation (3) devient
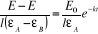 (II-15) (II-15)
où
 (II-16) (II-16)
ou encore

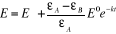 (II-17) (II-17)
E
O
t
A >
B
E
O
t
B >
A
L'évolution de E en fonction du temps donne
les figures suivantes :
| 


