ii. Test de Kurtosis

Afin de mesurer l'aplatissement des séries, nous
pouvons recourir à une comparaison des kurtosis k avec la valeur que
prend ce coefficient. La distribution est jugée normale lorsque (k=3).
S'il excède ce chiffre, la série est leptokurtique; elle est plus
pointue avec des queues de distribution plus épaisses que celle de la
loi normale. Sinon si (k<3), la distribution est platykurtique,
c'est-à-dire que celle-ci est plus aplatie que la distribution normale.
La formule de Kurtosis se présente comme suit :

On exprime le degré d'excès de Kurtosis de la
façon suivante :
iii. Test de
Jarque-Bera
Ce test peut être construit à partir de deux
variables (S et K'), qui sont supposées être normales et
indépendantes. Elles suivent en conséquence une distribution de
Khi-deux à deux degrés de liberté. On peut la formuler de
la manière suivante :
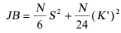
| 


