Résolution numérique des équations différentielles ordinaires linéaires

2.2.2 Méthode Runge-Kutta d'ordre 2 (RK2)

La méthode RK du deuxième ordre produit deux coéfficients K1_; K2 qui permettent d'écrire

	=
{K1 K2	=
Yn+ 1	=

_h

h:f (x_n; yn) l
h:f (x_n + _2;yn + 21 I

+ xl+K2 /

Yn 2

:

2.2.3 Méthode Runge-Kutta d'ordre 4 (RK4)

On applique la méthode de Runge-Kutta d'ordre plus élevé (RK4) pour obtenir plus de précision ; mais en doublant le temps de calcul puisqu'on procède de 4 évaluations de f.

{

K1 = h:f (xn; yn) h K1 K2 = h:f(~ xn+2;yn+ 2 h K2 K3 = h:f(xn+2;yn+ 2 K4 = h:f (xn + h;yn + K3)

:

K4

K2

6

3 +

K1 + 6

K3 + 3

yn+1 = y_n +

Exemple 2.2.1 On considère l'exemple (2.1.1) et on applique la méthode de Runge-Kutta d'ordre 2 (RK2).

On a :

h h

yn+1 = y_n + hf(x_n + _2;yn + ₂f(x_n;y_n))

Alors, pour n = 0 :

h h

y1 = y0 + hf(x0 + 2 ; y0 + ₂ f(x0_; y0))

0:05 0:05

= 1 + 0:05f(0 + 2 ; 1 + ₂ f(0;1))

= 1 + 0:05f(0:025_; 1) = 0:9975

2.3 La convergence des méthodes numériques 14

e, = jy (x_n) - ynj

En suivant les mêmes étapes de calcul, on obtient le tableau suivant :

x,

0

0:05

0:10

0:15

0:20

0:25

0:30

0:35

0:40

0:45

0:50

y,

1:0000

0:9975

0:9900

0:9777

0:9607

0:9393

0:9138

0:8846

0:8520

0:8165

0:7786

y0 ,

1:0000

0:9975

0:9900

0:9778

0:9608

0:9394

0:9139

0:8847

0:8521

0:8167

0:7788

avec y, est la solution approchée, et y0 , est la solution exacte du problème de Cauchy (2.1.3).

Remarque 2.2.1 On remaque que les solutions obtenues sont très proches de la solution exacte, voir figure 2.

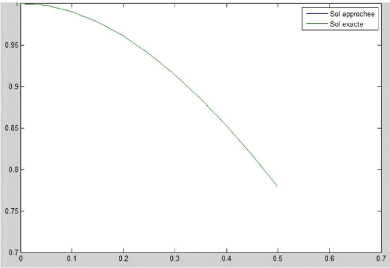
Figure 2