Application des méthodes de l'analyse de données sur l'évolution du parc automobile algérien

6. Test de validation

Graphique et table des inverses des racines

AR Root(s) Modulus Cycle

0.331481 0.331481

No root lies outside the unit circle. ARMA model is stationary.

MA Root(s)	Modulus	Cycle
-0.849570 #177; 0.490500i	0.980999	2.400000
0.000000 #177; 0.980999i	0.980999	4.000000
0.490500 #177; 0.849570i	0.980999	6.000000
0.849570 #177; 0.490500i	0.980999	12.00000
0.980999	0.980999
-0.490500 #177; 0.849570i	0.980999	3.000000
-0.980999	0.980999

No root lies outside the unit circle. ARMA model is invertible.

USTHB Page 109

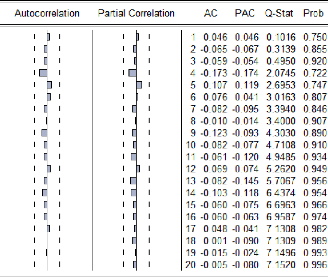
7. Test sur les résidus

Autocorrélations simples et partielles des résidus

Corrélogramme des résidus

Le corrélogramme des résidus du modèle montre que les résidus forment un bruit blanc puisque toutes les Autocorrélations et les Autocorrélations partielles sont significativement nulles.

Chapitre VII Application de la méthode de Box & Jenkins

USTHB Page 110

? Test des points de retournements

Il s'agit de tester : l'hypothèse nulle H0 : «les åi sont aléatoires» contre H1 « il existe une corrélation entre les åi i=1,..., n ».

Le nombre de points de retournements égale à p= ? = 28
On a n=38 et on a calculé E(p), Var(p) et S

E(p)= (n-2) =29.333 Var(p)= = 7.855 |T | = v = 29.333

? _t

? ?

P ²

K i

= #177; ?=

_{Q n n}

( 2) 1 = _8.933

ⁱ _n - _i

|T| =1.546< 1.96 donc on rejette H0 au seuil 0.05. C'est-à-dire que les résidus sont non

corrélés.

_T?

? Test de nullité de la moyenne des résidus

L'hypothèse H0 : « m=0 » contre H1 : « m ? 0 », nous utilisons le test de Student basé sur la

statistique :

_n?1

La moyenne de la série : åt = -53.169 L'écart type : ót =794.530

La statistique t=0.448 qui suit asymptotiquement une loi de Student., Au seuil á=0.05 on a: |t|<1.96, on accepte H0, alors m=0.

? Test de Ljung -Box

Nous calculons la statistique de Ljung-Box avec MATLAB

au seuil 0,05

2 21.026

H0 : « les Autocorrélations ne sont pas significativement différentes de zéro

Jusqu'au pas k = N/ 4 » Contre H1 : « Pi, i=1,2..., K / Pi?0 ».

? ₀ . ₉ 5 _{(1 1)} ?

L'ordre de retard K= [N/4]= [47/4]=12

Au seuil á= 0.05 on a la valeur critique d'une

=9.215 < 21.026 alors les autocorrélations ne sont pas significatives jusqu'au pas

K=12

I.e. les résidus forment un bruit blanc.

? Test de Jaque -Bera

On test H0 :" accepter la normalité des résidus au seuil 0.05" Contre H1 :"il n'y a pas de normalité des résidus".

Chapitre VII Application de la méthode de Box & Jenkins

USTHB Page 111

On accepte l'hypothèse nulle H0 si JB <

On a la statistique JB= 77.070 >5.99 donc on rejette l'hypothèse de normalité des résidus.

? Test de Skewness (asymétrie) et de Kurtosis (aplatissement)

On test : « =0 et =0" contre : " 0 ou 0"

? Test de Skewness : = où : est le coefficient de Skewness

v

(l'indicateur d'asymétrie des résidus).

La statistique de SKEWNESS = 4.211 qui est asymptotiquement N(0,1)

Au seuil á= 0.05 on a: 4.211 > 1.96, Donc on rejette, la distribution des résidus n'est pas asymétriques.

Test de Kurtosis : = v où s2 est le coefficient de Kurtosis (degré

d'aplatissement de la loi des résidus).

La statistique de KURTOSIS = 7.702 qui est asymptotiquement N(0,1)

Au seuil á = 0.05

7.702 >1.96, alors on rejette l'hypothèse des queues de la distribution des résidus non chargées. Les résidus forment un bruit blanc non gaussien

REMARQUE Nous ne pouvons pas appliquer le test de Durbin-Waston et le test d'indépendance de Von-neumann puisque les résidus ne sont pas gaussiens

Chapitre VII Application de la méthode de Box & Jenkins

USTHB Page 112

? Test d'homoscédasticité des résidus

Soit les hypothèses :H0 :« les résidus sont homoscédastique »contre

H1 : « les résidus sont hétéroscédastique »

L'hypothèse nulle à tester est celle d'homoscédasticité H0 : « á1= á2=...= á_p=0 » .

Si H0 est acceptée, la variance conditionnelle de l'erreur est constante = á0.
Sinon les résidus suivent un processus ARCH(p) dont l'ordre p est à déterminer.

Corrélogramme simple et partielle des résidus au carrée

L'analyse du corrélogramme des résidus au carrée, montre que tous les termes sont significativement différents de zéro car les probabilités sont toutes supérieur à 0,05, cela veut dire qu'il n'ya pas un effet ARCH. Pour confirmer, nous sommes passées au test d'homoscédasticité dont le résultat est donné par Eviews5.

ARCH Test:

F-statistic 0.155699 Probability 0.695098

Obs*R-squared 0.162352 Probability 0.687000

Test Equation:

Dependent Variable: RESID^2

Method: Least Squares

Date: 05/09/11 Time: 13:30

Sample (adjusted): 1965 2009

Included observations: 45 after adjustments

USTHB Page 113

Chapitre VII

		Application de la méthode de Box & Jenkins
Variable	Coefficient	Std. Error t-Statistic	Prob.
C	556019.8	269442.0 2.063597	0.0451
RESID^2(-1)	0.059703	0.151305 0.394587	0.6951
R-squared	0.003608	Mean dependent var	592700.3
Adjusted R-squared	-0.019564	S.D. dependent var	1680138.
S.E. of regression	1696493.	Akaike info criterion	31.56945
Sum squared resid	1.24E+14	Schwarz criterion	31.64975
Log likelihood	-708.3127	F-statistic	0.155699
Durbin-Watson stat	1.984068	Prob(F-statistic)	0.695098

Rappelons que, sous l'hypothèse nulle d'homoscédasticité, la statistique du multiplicateur de Lagrange (n* R²) au seuil 5% suit une loi de khi-deux à p degrés de liberté. Dans notre cas p = 1.Nous avons (n* R²) = 0.155 est inférieure à ÷²(1) = 3.84, donc nous acceptons l'hypothèse nulle d'homoscédasticité en faveur de l'hypothèse alternative d'hétéroscédasticité conditionnelle (il n'y a pas effet ARCH).