8. Test de validation
Graphique et table des inverses des racines
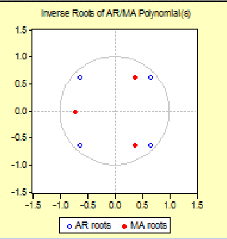
AR Root(s) Modulus Cycle
0.633023 #177; 0.633023i 0.895230 8.000000
-0.633023 #177; 0.633023i 0.895230 2.666667
No root lies outside the unit circle. ARMA model is
stationary.
MA Root(s) Modulus Cycle
-0.731765 0.731765
0.365882 #177; 0.633727i 0.731765 6.000000
No root lies outside the unit circle. ARMA model is
invertible.
A partir de la représentation graphique des inverses
des racines des polynômes de retards moyen mobile et
autorégressif, nous constatons qu'ils sont tous à
l'intérieur du cercle unité (les racines sont à
l'extérieur du cercle unité).
Chapitre VII Application de la méthode de Box &
Jenkins

USTHB Page 95
9. Test sur les résidus
Autocorrélations simples et partielles des
résidus

Corrélogramme des résidus
Chapitre VII Application de la méthode de Box &
Jenkins
USTHB Page 96
Le corrélogramme des résidus du modèle
montre que les résidus forment un bruit blanc puisque toutes les
Autocorrélations et les Autocorrélations partielles sont
significativement nulles.
? Test des points de retournements
Il s'agit de tester : l'hypothèse nulle H0
: «les åi sont aléatoires»
contre H1 « il existe une corrélation entre les
åi i=1,..., n ».
Le nombre de points de retournements égale à p= ? =
27
On a n=38 et on a calculé E(p), Var(p) et S
E(p)= (n-2) =24 Var(p)= = 6.43
|T | = v = 1.18
? t
T?
? ?
|T| =1.18< 1.96 donc on accepte H0 au seuil
0.05. C'est-à-dire que les résidus sont non
corrélés.
? Test de nullité de la moyenne des
résidus
L'hypothèse H0 : « m=0
» contre H1 : « m ? 0
», nous utilisons le test de Student basé sur la
n?1
La moyenne de la série : åt =
-0.027023
L'écart type : ót =2.110572
La statistique t=0.094953 qui suit
asymptotiquement une loi de Student. Au seuil á=0.05 on a: |t|<1.96,
on accepte H0, alors m=0.
? 2
K i
= #177; ?=
Q n n
( 2) 1 =1 1.903431
i n -
i
? Test de Ljung -Box
Nous calculons la statistique de Ljung-Box avec MATLAB
au seuil
0,05
Chapitre VII Application de la méthode de Box &
Jenkins
USTHB Page 97
H0 : « les Autocorrélations ne sont
pas significativement différentes de zéro
Jusqu'au pas k = N/ 4 »
Contre H1 : « Pi, i=1,2..., K / Pi?0
».
L'ordre de retard K= [N/4]= [47/4]=12
Au seuil á= 0.05 on a la valeur critique d'une
? 2 (2)
0 . 9 5
=11.903431< 24.995790
alors les autocorrélations ne sont pas significatives
jusqu'au pas K=15 I.e. les résidus forment un bruit blanc.
? Test de Jaque -Bera
On test H0 :" accepter la normalité des
résidus au seuil 0.05" Contre H1 :"il n'y a pas de
normalité des résidus".
On accepte l'hypothèse nulle H0 si
JB <
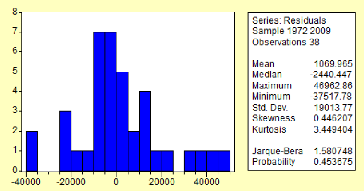
On a la statistique JB= 1.58 <5.99 donc on accepte
l'hypothèse de normalité des résidus.
? Test de Skewness (asymétrie) et de Kurtosis
(aplatissement) :
On test : « =0 et =0" contre
: " 0 ou 0"
/
? Test de Skewness : = I 1
s1 - 0 où : S11/2
est le coefficient de Skewness
1 6/n
(l'indicateur d'asymétrie des résidus).
Chapitre VII Application de la méthode de Box &
Jenkins
USTHB Page 98
La statistique de SKEWNESS = 1.12 qui est asymptotiquement
N(0,1)
Au seuil á= 0.05 on a:1.12 <1.96, alors on accepte que
la distribution des résidus ne sont pas asymétriques.
? Test de Kurtosis : = v où s2 est le
coefficient de Kurtosis (degré
d'aplatissement de la loi des résidus).
La statistique de KURTOSIS = 0.56 qui est asymptotiquement
N(0,1)
Au seuil á = 0.05.
On a: 0.56 <1.96, alors on accepte l'hypothèse des
queues de la distribution des résidus non chargées.
Les résidus forment un bruit blanc gaussien (suit une loi
Normal). ? Test de Kolmogorov - Smirnov
Nous testons H0 : « F=F0 » vs H1 : « F?F0
» où F0 est la fonction de répartition de la loi normal.
La statistique de Kolmogorov - Smirnov notée Dn =SUP
(|Dn+|, |Dn-|)=0.10.le seuil critique pour ce test est dc=0.22.
On a Dn< 0.22 au seuil 0.05. Donc,
on accepte l'hypothèse que les résidus sont gaussiens.
? Test d'indépendance de Von - Newman
L'hypothèse à tester est :
H0 : « les résidus sont
indépendants et identiquement distribués ».
H1 : « au moins deux observations
successives tendent à être corrélées positivement
».

|
S2?
|
1 ? ? ? ? ?
47 2 2
2
? ? D ? 1 ?? 46 ? ? ? ?
?
i 1 i
n ? 1 1 ? 1
? i i i
n 1
|
Chapitre VII Application de la méthode de Box &
Jenkins
USTHB Page 99
La variance corrigé S2=
352009710.494254.
La statistique D2 =
779221306.474829.
La statistique de Von_Neumann |?|= 0.676279 <1,96, nous
acceptons l'hypothèse H0. Les résidus sont indépendants et
identiquement distribués.
Test de Durbin -Watson (test de détection
d'autocorrélation d'ordre 1)
Nous testons H0 : « ñ=0 » vs
H1 : « ñ?0 ».

On a la statistique de Durbin - Watson : DW=2,206 d'après
le tableau ci-dessus. Avec du, á/2<DW<4-du,á/2
et du,á/2 =1,69 c.-à-d. on accepte
H0 :« les résidus sont non corrélés
».
| 


