II.1.5. LA GESTION PAR POINT DE
COMMANDE.
a) Introduction.
La gestion par point de commande se caractérise
par :
- un montant de commande constant ; cette quantité
économique de commande sera notée
« q » ;
- une périodicité de commande variable
(lorsqu'on est en univers aléatoire) ; on commande lorsque le stock
passe en dessous du point de commande « S »
Nous allons examiner successivement les deux cas de la figure
que sont :
· la gestion (q, S) en univers certain : ici la
demande est certaine, on commande avant rupture de stock et il n'y a pas de
coût de rupture. La variable de décision q, le montant de commande
sera déterminée de manière à minimiser le
coût de gestion qui ne comprend que deux termes : C(q) = Cc.Ic(q) +
Cp.Ip(q) (2.7)
· la gestion (q, S) en univers incertain. Dans ce cas, le
coût de rupture intervient aussi. Les variables de décision que
sont q, le montant des commandes et S, le point de commande seront
déterminés de manière à minimiser le coût de
gestion qui comprend trois termes :
C(q,S) = Cc.Ic(q, S) + Cp.Ip(q, S) + Cr.Ir(q, S) (2.8)
b) La gestion (q, S) en univers
certain.
Il s'agit de répondre aux questions :
- quand commander ?
- quelle quantité « q » à
commander périodiquement pour que le coût annuel moyen soit
minimum ?
Répondre à la première question
équivaut à trouver le point de commande tel que : S = D.L
(2.9)
Avec : D = demande annuelle
L = délai d'obtention exprimé en
année
Répondre à la seconde question équivaut
à déterminer la quantité optimale par la formule de
WILSON : 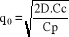 (2.10) (2.10)
c) La gestion en univers incertain.
La fonction de coût à minimiser fait intervenir
les trois variables d'état qui sont : Ic, Ip, et Ir
Sachant que dans l'expression (2.8), le nombre moyen de
commande dépend essentiellement de la quantité commandée
« q » tandis que le nombre moyen de rupture dépend
essentiellement du point de commande S. on peut donc réécrire
cette expression comme suit :
C(q,S) = Cc.Ic(q) + Cp.Ip(q, S) + Cr.Ir(S) (2.11)
On voit que le terme qui lie le problème en la variable
« q » et le problème en la variable «S»
est le stock moyen possédé Ip qui dépend à la fois
de « q » et de « S ». on ne
déterminera une solution approchée en séparant le
problème à deux variables en deux problèmes à une
variable de la manière suivante ; le principe pour obtenir cette
solution approchée est de résoudre indépendamment les deux
problèmes suivants :
- la détermination de la quantité
économique « q » en arbitrant entre le coût de
commande et le coût de possession à partir de la demande moyenne
comme si on était en univers certain.
- La détermination du point de commande S en arbitrant
entre le coût de rupture et le coût de possession en utilisant la
gestion calendaire pendant le délai d'obtention L, en retenant comme S
le niveau de recomplètement optimal.
Le problème de la détermination de la
quantité économique de commande n'est rien d'autre que le
problème étudié en univers certain si l'on remplace la
demande annuelle certaine par la demande annuelle moyenne : D = u
En minimisant le coût de gestion : C(q) = Cc.Ic(q)
+ Cp.Ip(q)
Où 
Le problème de la détermination du point de
commande « S » est quant à lui résolu en
prenant pour point « S » le niveau de recomplètement
qui minimise le coût d'une gestion calendaire durant le délai
d'obtention L :
C(S) = Cc.Ic(S) + Cp.Ip(S) avec P(X>S0) =  (2.12) (2.12)
| 


